Graphical Perception in a Pandemic

Log Scales, Exponential Growth, and the Importance of User Testing

Outline

1. A Short History of Pandemic Charts

2. Full-spectrum Graphics Testing

3. Challenges of Full-spectrum Testing

Slide Link

Pandemic Graphics:
🕰️History and Present Day💻

1918 Flu Pandemic

Reproduction from the Journal of the American Medical Association, Jan 11, 1919. Image source

1918 Flu Pandemic

All-cause mortality in Major Cities, 1918-1919 Image source

1840s London:

Cholera Mortality and Temperature

Excess Mortality and Temperature, 1840s London. From Report on the mortality of cholera in England, 1848-49, by William Farr (1952). Image Source

Cholera & Plague in London

Cholera & Plague in London (Created 1852) Image source

COVID-19 Graphics

May 6 2020: Three graphs that show a global slowdown in COVID-19 deaths, Image Source

COVID-19 Graphics

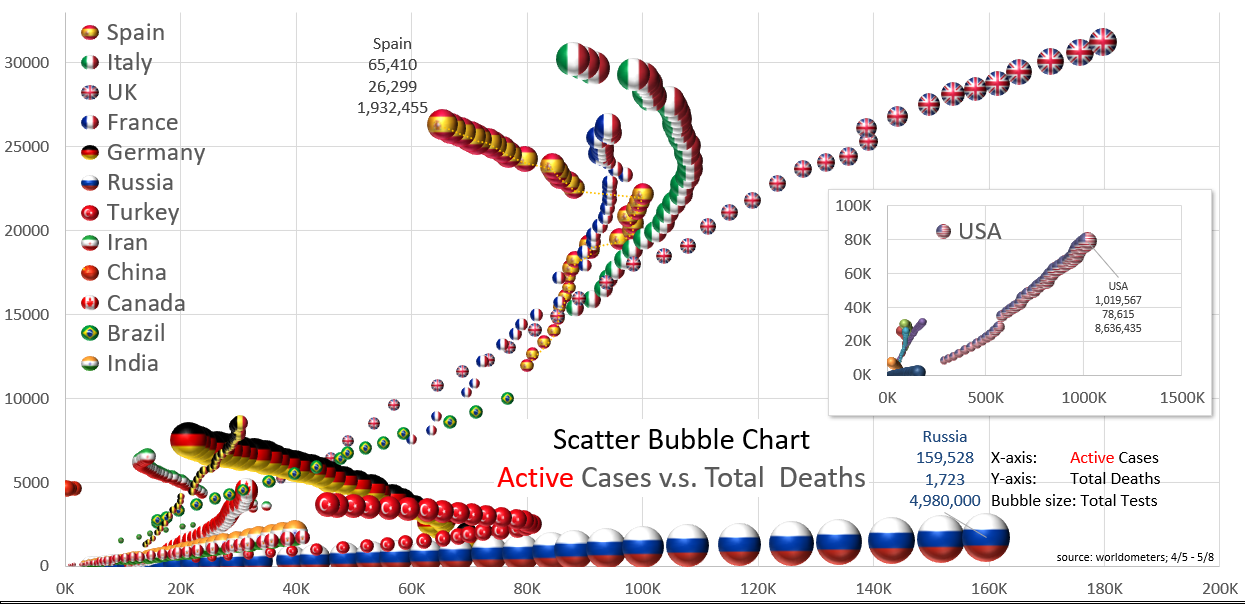
Active Cases vs. Total Deaths, Reddit, May 9 2020 Image source

COVID-19 Graphics

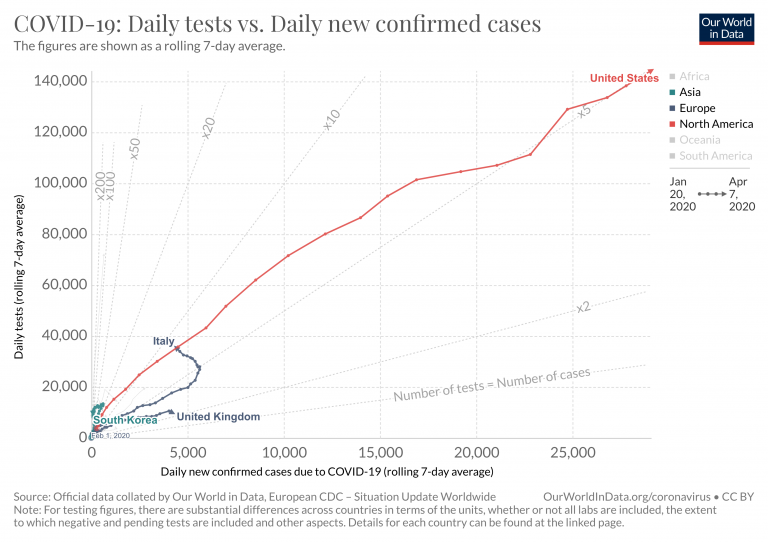
Tests vs. Cases, Our World in Data (May 19 2020)

COVID-19 Graphics

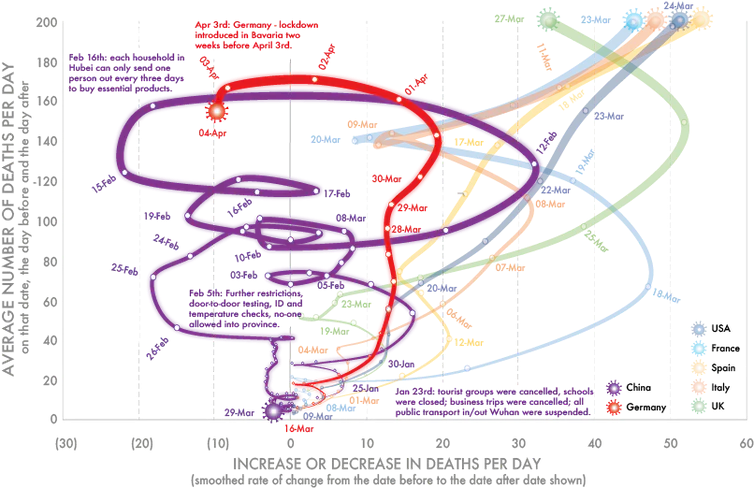
Rate of Death Change, March 28, 2020. Romain Vuillemot (@romsson) Image source

COVID-19 Graphics

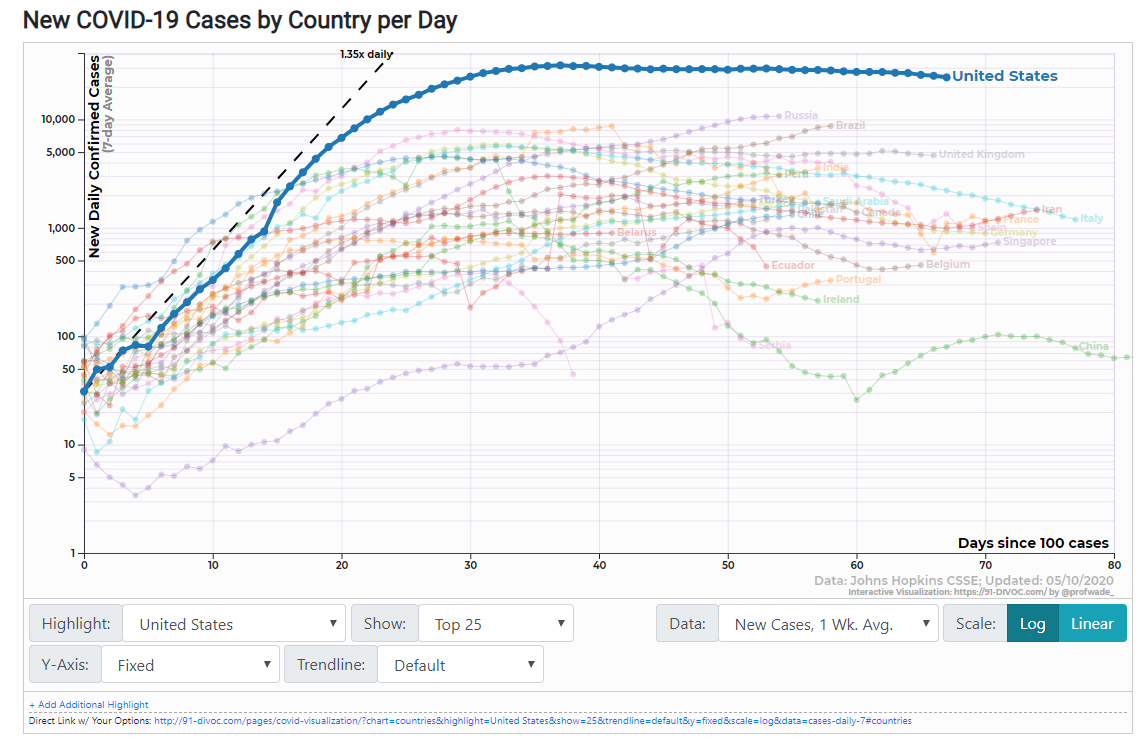
91-DIVOC Diagonal Reference Lines. May 11, 2020.

COVID-19 Graphics

Financial Times March 23, 2020. John Burn-Murdoch Image source

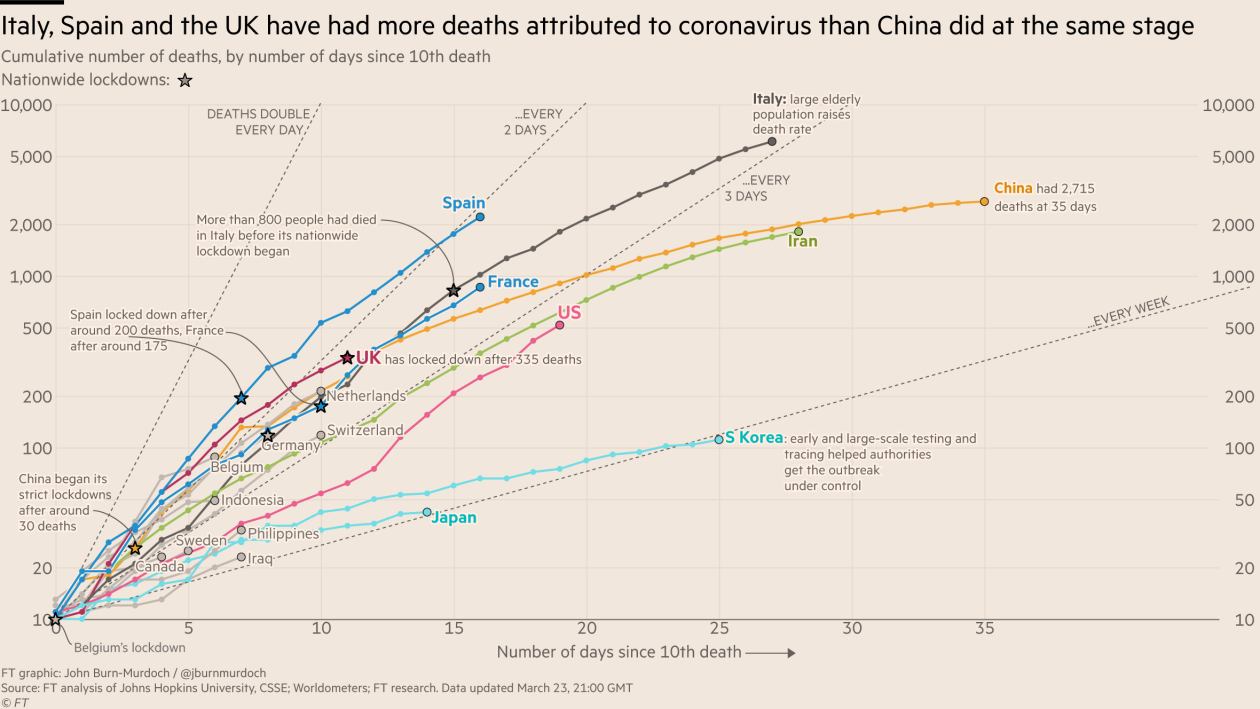
COVID-19 Graphics

The complexity of log scales. Nov 12, 2020. Mark Gubrud (@mgubrud) Image source

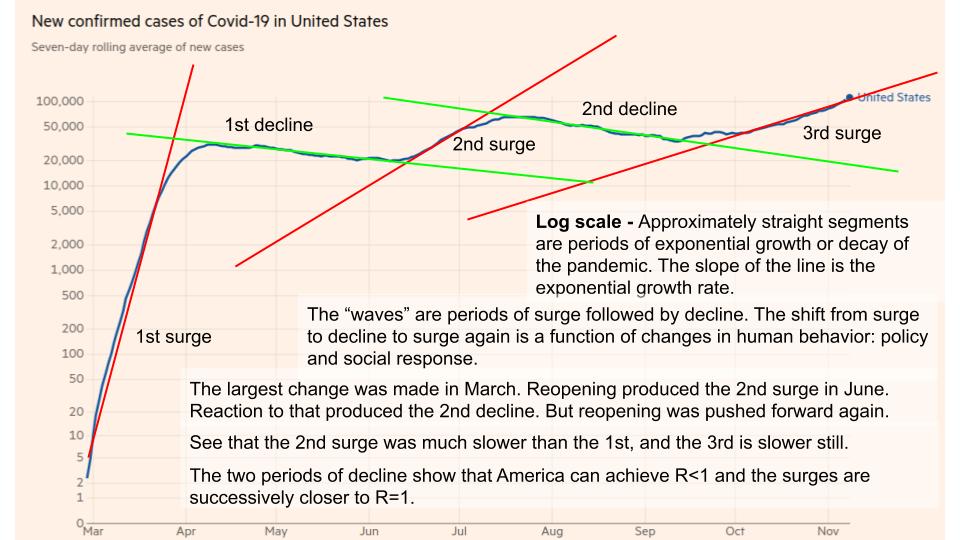
Exponential Growth

What is the purpose of this chart?

To help people predict what is likely to happen?

(It doesn’t do that very well)

Note that even if the growth is polynomial, we would still end up underestimating the number of cases. So if our goal is to help people make good decisions (like, hey, cases are increasing exponentially, I should stay home), then a graph like this may not be the best way to go about it, because we know for a fact that people don’t make effective forecasts from these types of plots.

The natural way to correct for graphs showing exponential growth is to use a log y-axis scale, which solves some problems and creates a whole host of new problems.

Exponential Growth

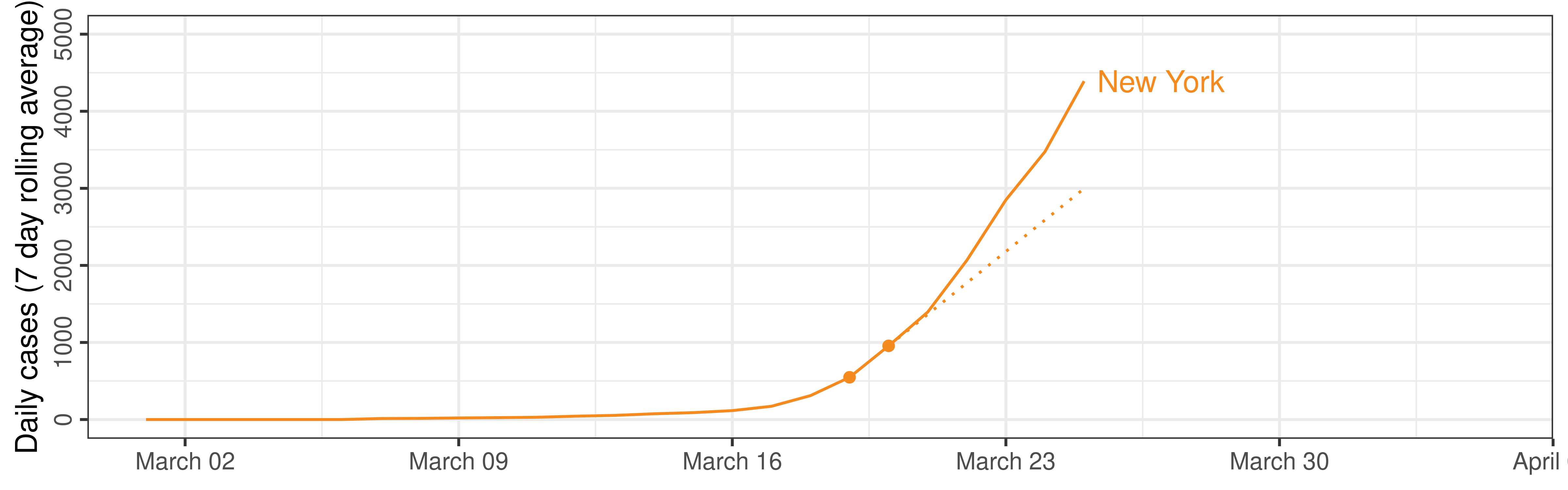
What is the purpose of this chart?

To help people predict what is likely to happen?

Humans are awful at predicting exponential growth
Wagenaar and Sagaria (1975; Timmers and Wagenaar 1977)

Note that even if the growth is polynomial, we would still end up underestimating the number of cases. So if our goal is to help people make good decisions (like, hey, cases are increasing exponentially, I should stay home), then a graph like this may not be the best way to go about it, because we know for a fact that people don’t make effective forecasts from these types of plots.

The natural way to correct for graphs showing exponential growth is to use a log y-axis scale, which solves some problems and creates a whole host of new problems.

Representing Exponential(ish) Data

• Log or linear scales?

• Reference lines?

• Aligning x-axis to date? Days since ___ cases?

• “Pace” of the case counts vs. raw counts?

• Comparing across populations – size, policies, susceptibility…

Why Visualize Data? Communication!

To inform

• Numeric accuracy
• Comparative accuracy
• Overall trajectory

To aid individual decision-making

• Decision outcome supported by evidence?
• Risk vs. raw case counts
• Uncertainty quantification

To aid policy development

• Uncertainty quantification
• Risk/reward of different options

Different goals = different charts

How Do We Test Graphics?

The question is not What is the best chart?

but… What is the best chart for this purpose?

For an answer, we need to subject charts to a full spectrum of user tests.

Full-spectrum Graphical Testing
in Practice

Perception: Log Scales

3 different ways of engaging with the data

Can we

• Q1: perceive differences in     … Perceptual
• Q2: forecast trends from     … Tactile
• Q3: estimate and use     … Numerical

graphs of exponential growth with log and linear scales?

300 participants completed all 3 experiments

I’m a huge fan of lineups, but one of the issues I had with the COVID graphs I was seeing was that I wasn’t convinced people were interpreting the data correctly.

I started thinking about why lineups wouldn’t test things at the level I was hoping for, and eventually came up with this hierarchy - first, you have to be able to recognize that there is a difference between two things. Then, you have to be able to predict and forecast to map “data from the past” onto the future. Finally, you have to actually be able to read data off of the graph and act on it - doing numerical calculations and the like.

These are distinct psychological tasks, and they require different ways of interacting with a chart. So I’m going to describe 3 experiments that we’ve conducted relating to log scales.

These experiments were inspired by COVID, but we worked hard to not go anywhere near COVID data because while we were designing these experiments, it was a bit emotionally loaded. Even now that pandemic measures have ended, it’s still too politically sensitive to touch, so we’ll continue using non-covid data on follow-up studies.

Q1: Perception of Differences

Q1: Perception of Differences

Log Scale

Linear Scale

Our first level of engagement is basic perception - can we actually distinguish different growth rates/levels of curvature on a linear and log scale. This is the most basic thing – if we can’t do this, then we probably won’t be able to predict things well or read information off the graph well (though, that last point is arguable).

• Factorial Experiment:
  • Log/linear scale (2 levels)
  • Lineup composition: (6 levels)
    • Target plot - high, medium, low curvature
    • Null plots - high, medium, low curvature
    • Exclude combinations where target/null are the same
  • Low/High variability (2 levels)
• Included 6 Rorschach plots (3 curvature levels x log or linear scale)

12 lineups + 1 Rorshcach plots = 13 evaluations per person

Here are a couple of example lineups from this experiment - the first is on a linear scale, the 2nd is on a log scale. While I generally tried throughout these experiments to make it clear that we were on a log scale, it is a very subtle difference in these lineups, and fixing that wasn’t necessarily relevant to the question at hand – since all sub-panels have the same axis breaks, we’re actually testing whether we can distinguish the data, not the scales.

Q1: Perception of Differences

Conclusion: It’s easier to spot a curve among lines than it is to spot a line among curves

Robinson, Howard, and Vanderplas (2023a)

We used a generalized linear mixed effects model to assess the probability of a correct target identification given factors like target and null plot type, participant skill level, and random effects due to the data generating process. The plot shown here is the resulting log odds ratio for log vs. linear scales, and we see that it is easier to detect curvature among a field of null lines than it is to detect linearity among a field of curved lines. In addition, we see that when there is a lot of contrast between the null and the target plot, that is, when the nulls are very curved and the target is very straight, there isn’t much difference between the two graphs. However, if there is less contrast, the log scale allows us to perceive the differences better than the linear scale.

• Log scales make us more sensitive to slight changes in curvature:
  • Low Curvature Null vs. Medium Curvature Target on log scale is curve vs. line
    (it’s hard to see the straight-line target vs. the curved nulls)
  • With Medium or High curvature Null plots, it’s easier to spot the target on the log scale than on the linear scale

Q2: Forecasting Exponential Trends

The next question we had was whether we can accurately predict/forecast exponential trends. This study is quite different from the last one - users were asked to draw lines on graphs interactively.

Q2: Inspiration

• D. J. Finney (1951) Subjective Judgment in Statistical Analysis: An Experimental Study. Journal of the Royal Statistical Society

• Frederick Mosteller et al. (1981) Eye Fitting Straight Lines. The American Statistician

• New York Times’ ‘You Draw It’ features:

  • Family Income affects college chances
  • Just How Bad Is the Drug Overdose Epidemic?
  • What Got Better or Worse During Obama’s Presidency

There have been a number of statistical experiments with “eye fitting” regression models. The first was driven by the desire to reduce computation time; the second is much more psychological in nature. That study had students line up a transparency with a straight line on it to fit a regression line to some data. They found that students tended to fit the slope of the first PC rather than the least squares line.

More recently, The New York Times has used a really cool setup to have people predict data before showing them the actual trend. They use javascript and have people draw directly on the plot. The line can be curved, jagged, etc. - it’s not restricted to a strictly linear set-up. We decided to adopt this approach because we didn’t want to impose a specific functional form, because it’s not totally clear that people are thinking exponentially or are actually good at drawing exponential curves.

The methods changed a bit, but the basic concept is the same.

Q2: Forecasting (You-Draw-It) Goals

1. Replicate Eye Fitting Straight Lines using the you-draw-it tool (4 charts) Robinson, Howard, and Vanderplas (2022)

2. Explore exponential growth predictions on log and linear scale (8 charts)

   • Points end 50% or 75% of the way across x-axis
   • Rate of growth of \(\beta\) = 0.1, 0.23
   • Log or Linear scale

12 total graphs to complete

First, we wanted to validate the “Eye fitting straight lines” method using You Draw it, by using datasets from the 1981 study, on the original linear scale. This would serve as a validation of the method and also help us test out our analysis method on data that was a bit more straightforward.

Then, the (main) goal is to see how terrible we are at predicting exponential growth when using a log scale and a linear scale.

We set things up with varying amounts of data – so you have data to base your regression line up to either halfway or 3/4 of the way through the graph, and you have to then extend beyond the data by 25% or 50%.

We used two different rates of growth, and then either had a graph with a log or linear scale.

If you’re keeping track, then there are 4 straight lines, and 8 sets of exponential data (generated on the fly from basic parameters). We saved both the data shown on the plot and the drawn smooth lines.

Q2: Forecasting (You-Draw-It)

Data from Mosteller et al. (1981)

Exp data, linear scale, 50% complete

Q2: Forecasting (You-Draw-It)

Here, I’m showing you the actual drawn lines for each of the exponential conditions, and you can see that there are a few interesting features:

1. Not everyone drew very smooth lines – we probably need to do some data cleaning based on the number of sharp “jumps” in the data – possibly excluding those cases or smoothing over them.

2. The amount of deviation in the final prediction value is (surprisingly) not much larger when there is less data – this was really shocking for me

3. Linear scale predictions seem to be lower than log scale predictions, in particular when beta is higher – it’s not that noticeable when beta is low. So the under-prediction bias is stronger for linear scales than it is for log scales. That doesn’t necessarily mean that everyone underpredicts, but you do see way more orange lines on top in the lower right panel.

Q2: Forecasting (You-Draw-It)

If we look at the residuals instead, we see that there is still some under-prediction even with the log scale when beta is high, but our basic conclusions from the original plots still hold.

Q2: Forecasting (You-Draw-It)

We can make this even clearer by modeling the residuals using a generalized additive model, which has a flexible form and doesn’t require too many assumptions about model structure.

Q3: Numerical Estimation

Q3: Numerical Estimation

• Next level of engagement is estimating quantities from a graph

• This is a much harder experiment to set up

  • Phrasing matters a lot!
  • Data matters a lot!

How to make it generalizable?

One of my favorite parts of graphical inference is that it totally sidesteps this question of phrasing by encoding all of what would have been verbal questions into the graph itself.

This really is a huge improvement over past graphical methods – there were studies showing that pie charts sucked from the early 1900s, but they were hampered by the generalizability of the questions - if you asked for someone to estimate the percentage of a pie slice, you got different conclusions than if you asked someone to make a judgement between two pieces of the pie.

Q3: Numerical Estimation

• Use Ewoks and Tribbles - creatures that might multiply exponentially
• One set on the linear scale, one set on log scale
• Underlying trend is the same (within transformed x axis)
• Different variability around the line

Ewoks and Tribbles (with apologies to Allison Horst)

Q3: Numerical Estimation

Free response: Between \(t_1\) and \(t_2\), how does the population of \(X\) change?

 

Linear Scale

 

Log Scale

 

Q3: Numerical Estimation

Estimating Population given a year

Process Sketch

Linear scale

Log scale

Q3: Numerical Estimation

Estimating Population given a year

Deviation from Closest Point

• More variability in estimation on linear scale (which makes sense due to the fact that it’s compressed into a small area of the plot)

• Participants anchor estimates to specific points, not to an overall fitted trend

Q3: Numerical Estimation

From Year1 to Year2, the population increases by ____ individuals

Process Sketch

Linear scale

Log scale

Q3: Numerical Estimation

From Year1 to Year2, the population increases by ____ individuals

• in dataset 1, both points were close to the underlying value, and the estimates bear that out.

• in dataset 2, one point was a bit of an outlier, and so we can see different estimation strategies appear: some participants answered using an overall trend/visual regression, while others answered using actual points.
  

Q3: Numerical Estimation

How many times more creatures are there in Year2 than Year1?

Process Sketch

Linear scale

Log scale

Q3: Numerical Estimation

How many times more creatures are there in Year2 than Year1?

• the results show a fundamental lack of understanding on the part of many participants

Q3: Numerical Estimation

How many times more creatures are there in Year2 than Year1?

• When we look only at people who answered in a reasonable range given the question (e.g. didn’t assume we meant additive estimation), we see a lot of variability and a few more things to look into here - such as why there’s a peak in dataset 1 that is around 15, even though the closest point and the true value are both near 10.

Q3: Numerical Estimation

How many times more creatures are there in Year2 than Year1?

• As the questions get more mathematically complex, we also see that participants start using model-based strategies for estimation - they don’t have the mental bandwidth to hold all of the estimates for specific points, arithmatic, etc. in their heads, so they take shortcuts like working off of a mental trendline.

• Here, for the first time, the true deviation (deviation from the underling model) is a better match to participant estimates than the closest point deviation.

Q3: Numerical Estimation

How long does it take for the population in Year 1 to double?

Process Sketch

Linear scale

Log scale

Q3: Numerical Estimation

How long does it take for the population in Year 1 to double?

• strong anchoring effect at multiples of 5

• Some conflict between true and closest point value in dataset 1 (mediated by rounding tendencies); dataset 2 was clear enough that participants could estimate 6

• a lot more variability on the linear scale than the log scale in both cases

Challenges & Benefits of Full-spectrum Graphical Testing

Challenges & Benefits

1. Conflicting results can be hard to reconcile

2. Conducting multiple studies is multiple times the work
   (multiple times the payoff?)

3. Greater insight into the tradeoffs of design decisions

Challenges & Benefits

• Testing method needs to match level of engagement

• Examine graphical choices across engagement levels

Packages

References

Bajgier, Steve M., Maryanne Atkinson, and Victor R. Prybutok. 1989. “Visual Fits in the Teaching of Regression Concepts.” The American Statistician 43 (4): 229–34. https://doi.org/10.1080/00031305.1989.10475664.

Buja, Andreas, Dianne Cook, Heike Hofmann, Michael Lawrence, Eun-Kyung Lee, Deborah F Swayne, and Hadley Wickham. 2009. “Statistical Inference for Exploratory Data Analysis and Model Diagnostics.” Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 367 (1906): 4361–83. https://doi.org/10.1098/rsta.2009.0120.

Cooke, L. 2010. “Assessing Concurrent Think-Aloud Protocol as a Usability Test Method: A Technical Communication Approach.” IEEE Transactions on Professional Communication 53 (3): 202–15. https://doi.org/10.1109/TPC.2010.2052859.

Croxton, F. E., and H. Stein. 1932. “Graphic Comparisons by Bars, Squares, Circles, and Cubes.” Journal of the American Statistical Association 27 (177): 54–60. https://doi.org/10.1080/01621459.1932.10503227.

Croxton, F. E., and R. E. Stryker. 1927. “Bar Charts Versus Circle Diagrams.” Journal of the American Statistical Association 22 (160): 473–82. https://doi.org/10.2307/2276829.

Eells, W. C. 1926. “The Relative Merits of Circles and Bars for Representing Component Parts.” Journal of the American Statistical Association 21 (154): 119–32. https://doi.org/10.1080/01621459.1926.10502165.

Gegenfurtner, Andreas, Erno Lehtinen, and Roger Säljö. 2011. “Expertise Differences in the Comprehension of Visualizations: A Meta-Analysis of Eye-Tracking Research in Professional Domains.” Educational Psychology Review 23 (4): 523–52. https://doi.org/10.1007/s10648-011-9174-7.

Goldberg, Joseph H., and Jonathan I. Helfman. 2010. “Comparing Information Graphics: A Critical Look at Eye Tracking.” In Proceedings of the 3rd BELIV’10 Workshop on BEyond Time and Errors: Novel evaLuation Methods for Information Visualization - BELIV ’10, 71–78. Atlanta, Georgia: ACM Press. https://doi.org/10.1145/2110192.2110203.

Goldberg, Joseph, and Jonathan Helfman. 2011. “Eye Tracking for Visualization Evaluation: Reading Values on Linear Versus Radial Graphs.” Information Visualization 10 (3): 182–95. https://doi.org/10.1177/1473871611406623.

Guan, Zhiwei, Shirley Lee, Elisabeth Cuddihy, and Judith Ramey. 2006. “The Validity of the Stimulated Retrospective Think-Aloud Method as Measured by Eye Tracking.” In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems - CHI ’06, 1253. Montréal, Québec, Canada: ACM Press. https://doi.org/10.1145/1124772.1124961.

Hegarty, Mary, Harvey S. Smallman, and Andrew T. Stull. 2012. “Choosing and Using Geospatial Displays: Effects of Design on Performance and Metacognition.” Journal of Experimental Psychology: Applied 18 (1): 1–17. https://doi.org/10.1037/a0026625.supp.

Hughes, B. M. 2001. “Just Noticeable Differences in 2d and 3d Bar Charts: A Psychophysical Analysis of Chart Readability.” Perceptual and Motor Skills 92 (2): 495–503.

Liu, Chan, Hao Liu, and Zhanglu Tan. 2023. “Choosing Optimal Means of Knowledge Visualization Based on Eye Tracking for Online Education.” Education and Information Technologies, May. https://doi.org/10.1007/s10639-023-11815-4.

Loy, Adam, and Heike Hofmann. 2013. “Diagnostic Tools for Hierarchical Linear Models.” Wiley Interdisciplinary Reviews: Computational Statistics 5 (1): 48–61. https://doi.org/10.1002/wics.1238.

Lu, Min, Joel Lanir, Chufeng Wang, Yucong Yao, Wen Zhang, Oliver Deussen, and Hui Huang. 2022. “Modeling Just Noticeable Differences in Charts.” IEEE Transactions on Visualization and Computer Graphics 28 (1): 718–26. https://doi.org/10.1109/TVCG.2021.3114874.

Majumder, Mahbubul, Heike Hofmann, and Dianne Cook. 2013. “Validation of Visual Statistical Inference, Applied to Linear Models.” Journal of the American Statistical Association 108 (503): 942–56. https://doi.org/10.1080/01621459.2013.808157.

Mosteller, Frederick, Andrew F. Siegel, Edward Trapido, and Cleo Youtz. 1981. “Eye Fitting Straight Lines.” The American Statistician 35 (3): 150–52. https://doi.org/10.1080/00031305.1981.10479335.

Netzel, Rudolf, Jenny Vuong, Ulrich Engelke, Seán O’Donoghue, Daniel Weiskopf, and Julian Heinrich. 2017. “Comparative Eye-Tracking Evaluation of Scatterplots and Parallel Coordinates.” Visual Informatics 1 (2): 118–31. https://doi.org/10.1016/j.visinf.2017.11.001.

Robinson, Emily A., Reka Howard, and Susan Vanderplas. 2022. “Eye Fitting Straight Lines in the Modern Era.” Journal of Computational and Graphical Statistics 0 (0): 1–8. https://doi.org/10.1080/10618600.2022.2140668.

———. 2023a. “Perception and Cognitive Implications of Logarithmic Scales for Exponentially Increasing Data: Perceptual Sensitivity Tested with Statistical Lineups.” Journal of Computational and Graphical Statistics Under Review. https://earobinson95.github.io/logarithmic-lineups/logarithmic-lineups-revisions.pdf.

———. 2023b. “‘You Draw It’: Implementation of Visually Fitted Trends with R2d3.” Journal of Data Science 21 (2): 281–94. https://doi.org/10.6339/22-JDS1083.

Timmers, Han, and Willem A. Wagenaar. 1977. “Inverse Statistics and Misperception of Exponential Growth.” Perception & Psychophysics 21 (6): 558–62. https://doi.org/10.3758/bf03198737.

VanderPlas, S, R C Goluch, and H Hofmann. 2019. “Framed! Reproducing and Revisiting 150-Year-Old Charts.” Journal of Computational and Graphical Statistics 28 (3): 620–34. https://doi.org/10.1080/10618600.2018.1562937.

Vanderplas, S, and H Hofmann. 2017. “Clusters Beat Trend⁉ Testing Feature Hierarchy in Statistical Graphics.” Journal of Computational and Graphical Statistics 26 (2): 231–42. https://doi.org/10.1080/10618600.2016.1209116.

VanderPlas, S, C Röttger, D Cook, and H Hofmann. 2021. “Statistical Significance Calculations for Scenarios in Visual Inference.” Stat 10 (1). https://doi.org/10.1002/sta4.337.

von Huhn, R. 1927. “Further Studies in the Graphic Use of Circles and Bars.” Journal of the American Statistical Association 22 (157): 31–36. https://doi.org/10.1080/01621459.1927.10502938.

Wagenaar, William A., and Sabato D. Sagaria. 1975. “Misperception of Exponential Growth.” Perception & Psychophysics 18 (6): 416–22. https://doi.org/10.3758/BF03204114.

Woller-Carter, Margo M., Yasmina Okan, Edward T. Cokely, and Rocio Garcia-Retamero. 2012. “Communicating and Distorting Risks with Graphs: An Eye-Tracking Study.” Proceedings of the Human Factors and Ergonomics Society Annual Meeting 56 (1): 1723–27. https://doi.org/10.1177/1071181312561345.

Xiong, Cindy, Cristina R. Ceja, Casimir J. H. Ludwig, and Steven Franconeri. 2020. “Biased Average Position Estimates in Line and Bar Graphs: Underestimation, Overestimation, and Perceptual Pull.” IEEE Transactions on Visualization and Computer Graphics 26 (1): 301–10. https://doi.org/10.1109/TVCG.2019.2934400.

Zhao, Yifan, Dianne Cook, Heike Hofmann, Mahbubul Majumder, and Niladri Roy Chowdhury. 2013. “Mind Reading: Using an Eye-Tracker to See How People Are Looking at Lineups.” International Journal of Intelligent Technologies & Applied Statistics 6 (4): 393–413. https://doi.org/10.6148/IJITAS.2013.0604.05.

Questions?

Testing Graphics

Lineups

Question: Can participants identify different growth rates on a linear scale?

A “Visual Hypothesis Test”

• Embed the question in array of charts

• Can people identify the different plot?

• Null model can be tricky to create

• Test statistic is the visual evaluation

Buja et al. (2009)
Loy and Hofmann (2013)
Majumder, Hofmann, and Cook (2013)
Vanderplas and Hofmann (2017)
VanderPlas et al. (2021)

Numerical Estimation

Eells (1926)

von Huhn (1927)

• Size of region?
  Eells (1926); Croxton and Stryker (1927); VanderPlas, Goluch, and Hofmann (2019)
• With scales?
  von Huhn (1927)
• Size of relationship compared to another region
  Croxton and Stein (1932)
• Very sensitive to question phrasing

Forced Choice

Which bar is larger? Hughes (2001)

Hegarty, Smallman, and Stull (2012)

• Force participants to answer a specific question

• May be a size judgment (which is larger?)

  • common in psychophysics experiments

• May be a more complex decision incorporating other information

Hughes (2001)
Xiong et al. (2020)
Lu et al. (2022)

Eye Tracking

• Infer cognitive processes from directed (conscious) attention

• May be accompanied by direct estimation or other protocols

Gegenfurtner, Lehtinen, and Säljö (2011)
J. Goldberg and Helfman (2011)
Zhao et al. (2013)
Netzel et al. (2017)
Liu, Liu, and Tan (2023)

J. H. Goldberg and Helfman (2010)

Woller-Carter et al. (2012)

Think Aloud and Free Response

• Stream of consciousness narration Guan et al. (2006; Cooke 2010)

• Reasoning to justify a decision

Why did you choose this panel? Vanderplas and Hofmann (2017)

Direct Annotation

Mosteller et al. (1981)

• Have participants visually fit statistics

  • Usually directly annotating the chart with e.g. a regression line

• Compare visual statistics to numerical calculations

• Differences tell us about our implicit perception of data
  e.g. visual regression is more robust to outliers

• Also useful as a teaching tool

Bajgier, Atkinson, and Prybutok (1989)
Robinson, Howard, and Vanderplas (2022)
Robinson, Howard, and Vanderplas (2023b)

How Do We Test Graphics?

• Testing method needs to be matched to level of engagement

• Need to examine graphical choices across levels of engagement