A Plot is Worth a Thousand Tests

Assessing Residual Diagnostics with the Lineup Protocol

Weihao (Patrick) Li, Di Cook, Emi Tanaka, Klaus Ackermann, Susan Vanderplas

2024-08-07

🔍 Regression Diagnostics

Diagnostics: is anything importantly wrong with my model?

\[\underbrace{\boldsymbol{e}}_\textrm{Residuals} = \underbrace{\boldsymbol{y}}_\textrm{Observations} - \underbrace{f(\boldsymbol{x})}_\textrm{Fitted values}\]

Residuals: what the regression model does not capture.

Checked by:

• Numerical summaries: variance, skewness, quantiles
• Statistical tests: F-test, BP test
• Diagnostic plots: residual plots, Q-Q plots

Diagnostic Plots

Residual plots are usually revealing when the assumptions are violated. –Draper and Smith (1998), Belsley, Kuh, and Welsch (1980)

Graphical methods are easier to use. –Cook and Weisberg (1982)

Residual plots are more informative in most practical situations than the corresponding conventional hypothesis tests. –Montgomery and Peck (1982)

🤔 Plot Interpretation Challenges

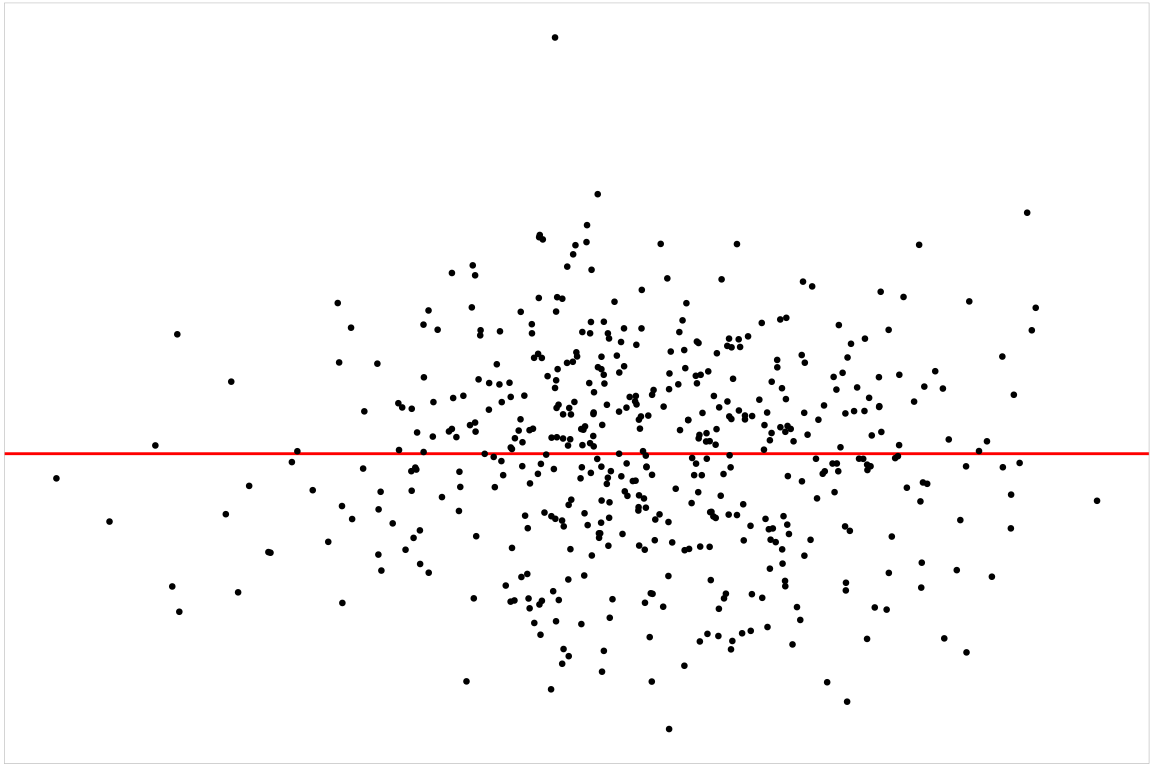
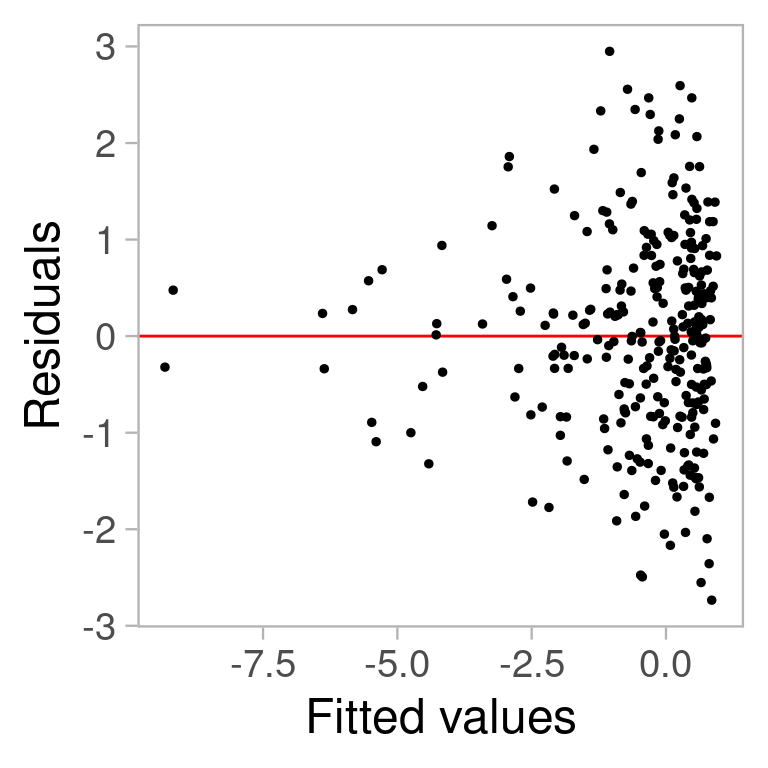
What do you see?

• Vertical spread of the points varies with the fitted values.
  => heteroskedasticity?

• Triangle shape is actually from skewed distribution in x
  Fitted model is fine!

We need an inferential framework to calibrate expectations when reading residual plots!

🔬 Visual Inference

Suggested by Buja et al. (2009)

What do you observe from this residual plot?

• Vertical spread of the points varies with the fitted values.

• This often indicates the existence of heteroskedasticity.

• The real data is in plot 11.

🔬 Visual Inference

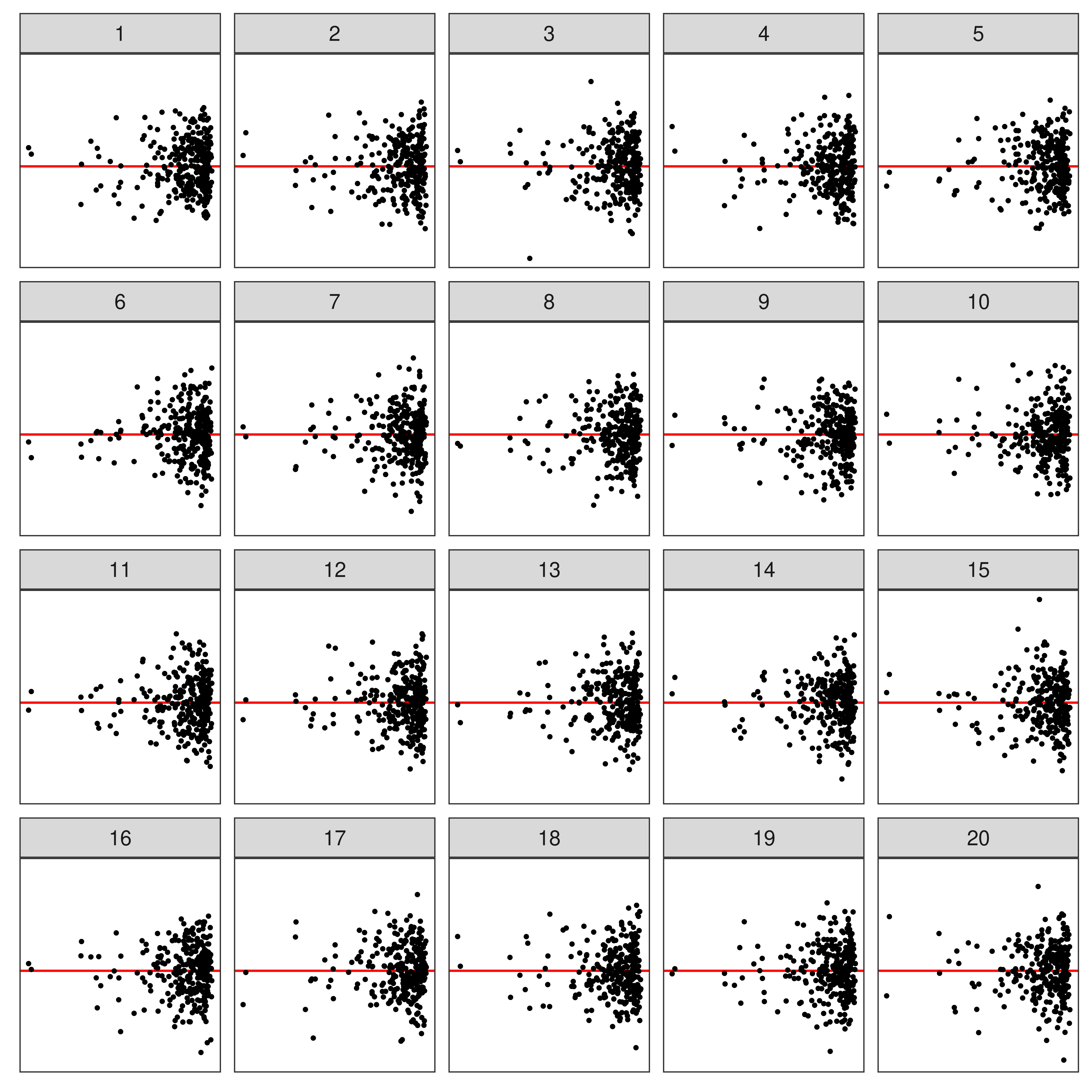
Typically, a lineup of residual plots consists of

• 1 data plot
• 19 null plots w/ residuals simulated from the fitted model.

🔬 Visual Inference

To perform a visual test

• Observer(s) select the most different plot(s).
• P-value (“see value”) can be calculated via a beta-binomial model (VanderPlas et al. 2021)

🧪 Experiment

Compare conventional hypothesis testing with visual testing when evaluating residual plots

🖊 Design

Model	Structure
Null	\(\boldsymbol{y} = \beta_0 + \beta_1\boldsymbol{x} + \boldsymbol{\varepsilon}\)
Non-linearity	\(\boldsymbol{y} = \boldsymbol{1} + \boldsymbol{x} + \boldsymbol{z} + \boldsymbol{\varepsilon}\)
Heteroskedasticity	\(\boldsymbol{y} = 1 + \boldsymbol{x} + \boldsymbol{\varepsilon}_h\)

where

• \(\boldsymbol{\varepsilon} \sim N(\boldsymbol{0}, \sigma^2\boldsymbol{I})\)
• \(\boldsymbol{z} \propto He_j(\boldsymbol{x})\), the \(j^{th}\) order probabilist Hermite polynomial
• \(\boldsymbol{\varepsilon_h} \sim N(\boldsymbol{0}, 1 + (2 - |a|)(\boldsymbol{x} - a)^2b \boldsymbol{I})\)

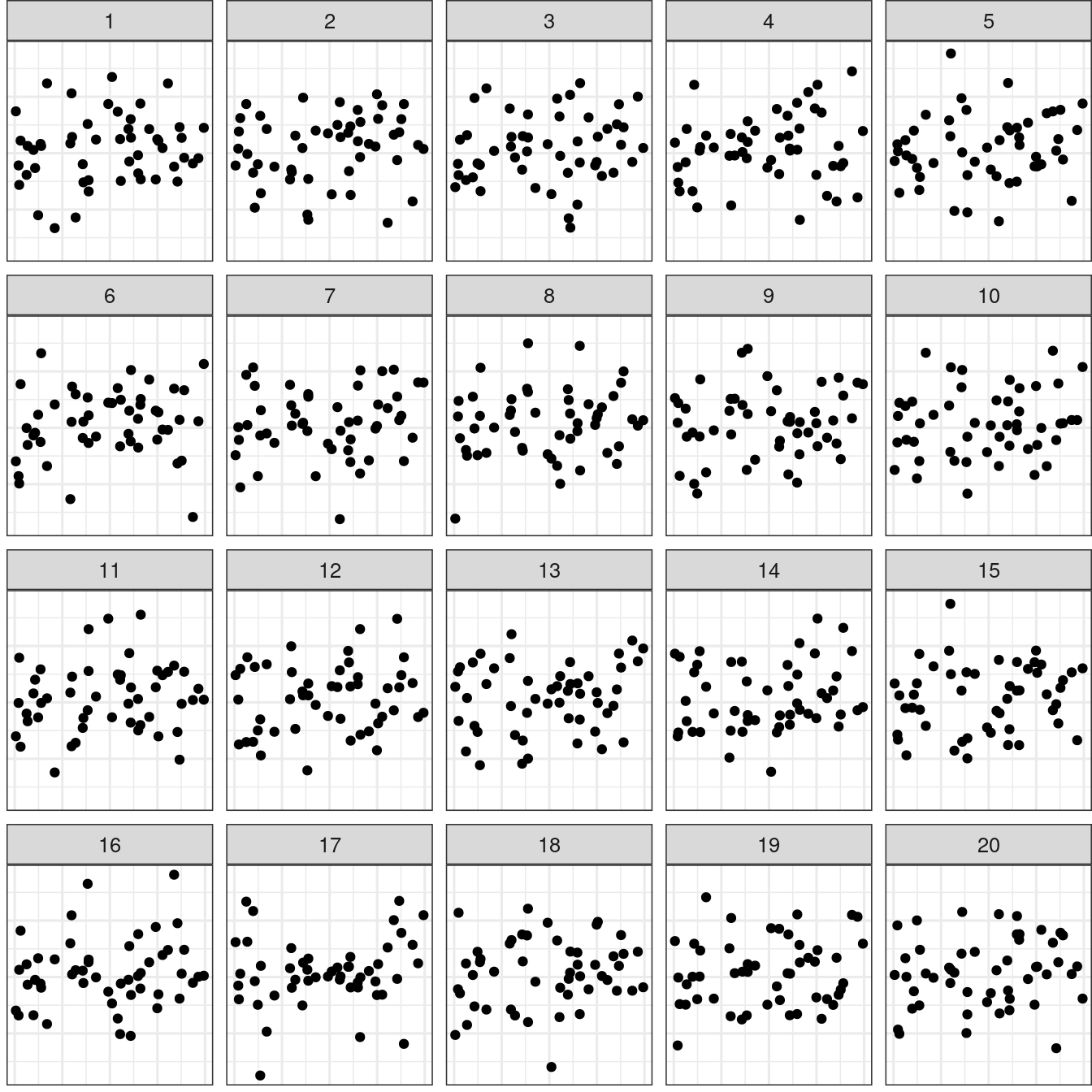
Non-linearity

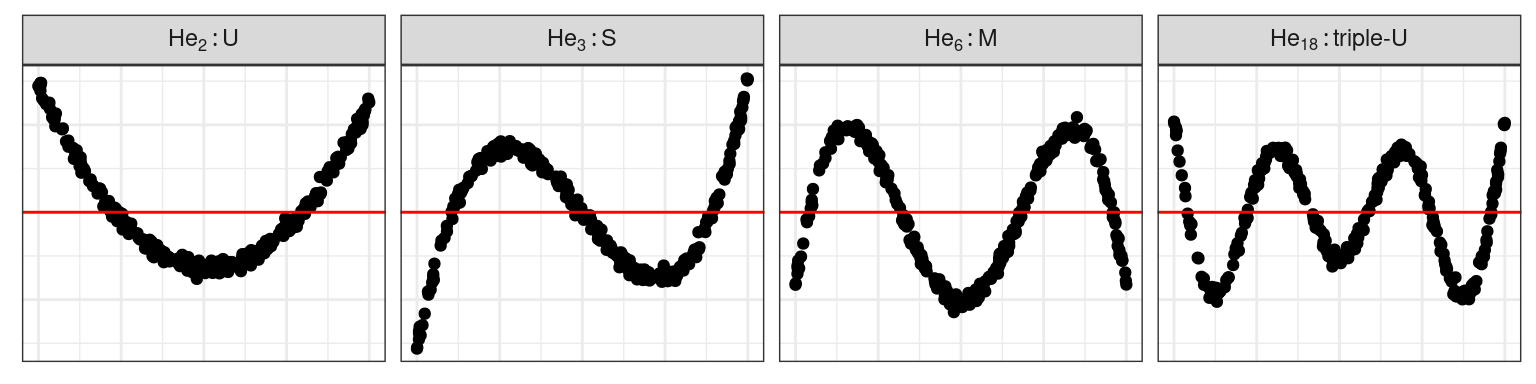
Heteroskedasticity

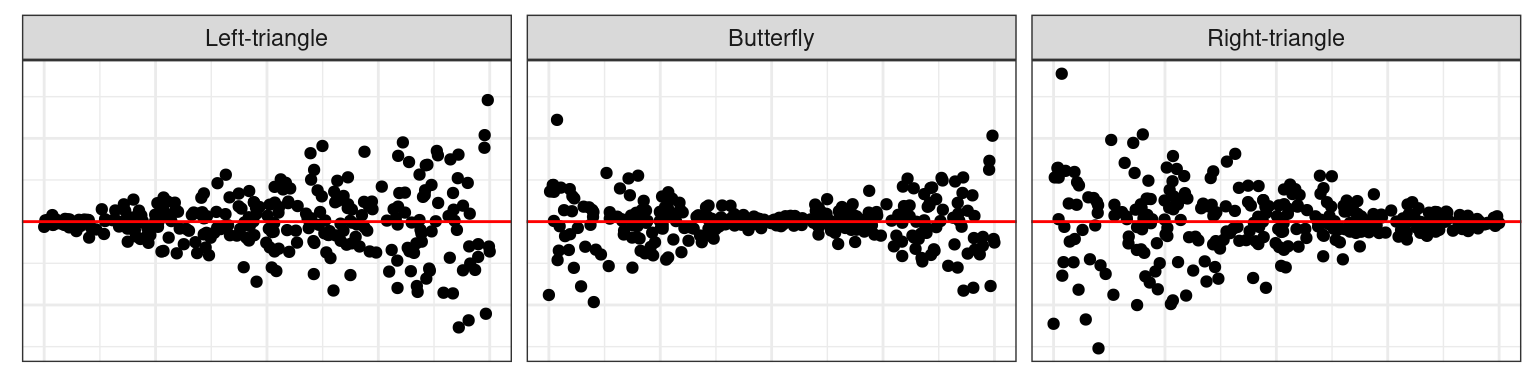
Lineup Generation

• parameters controlling signal strength (\(\sigma, b, n\))

• \(4\times 4\times 3 \times 4 = 192\) non-linear parameter sets

• \(3\times 5\times 3 \times 4 = 180\) heterosked. parameter sets

• 3 replicates per parameter set

• 576 (non linearity) + 540 (heteroskedasticity) lineups
  (w/ \(\geq\) 5 evaluations\()\))

• 36 Rorshach lineups to estimate \(\alpha\) for p-value calcs

📏 Effect size: Non-linearity

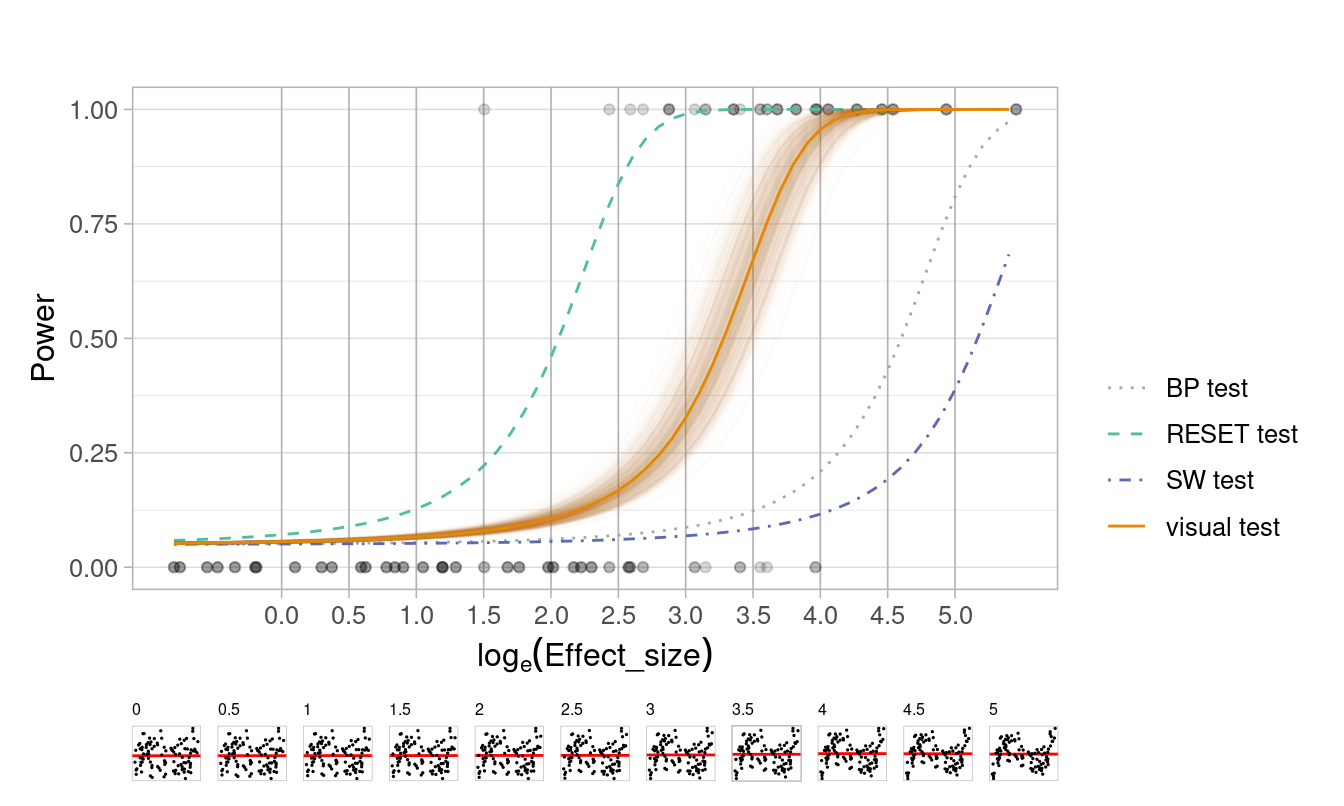
📏 Effect size: Heteroskedasticity

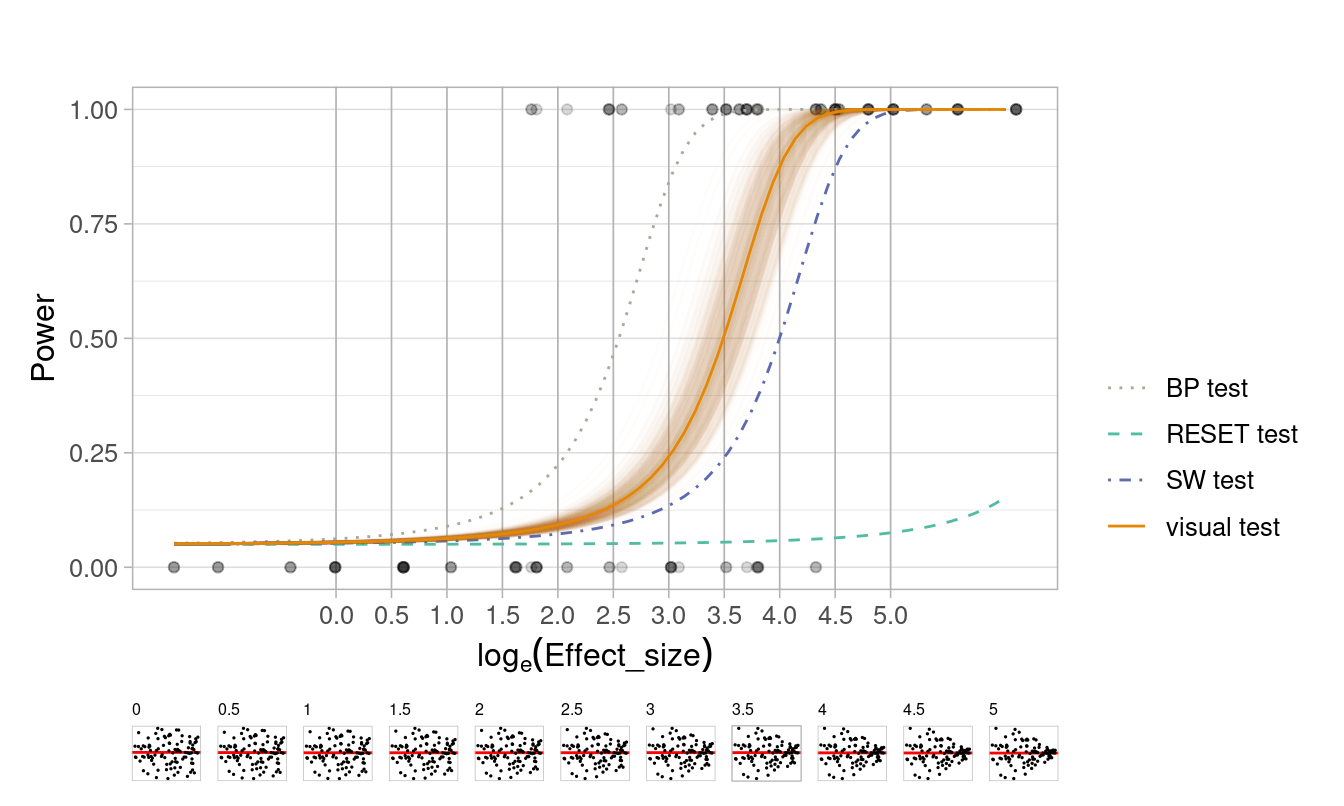
📊 Test Outcomes

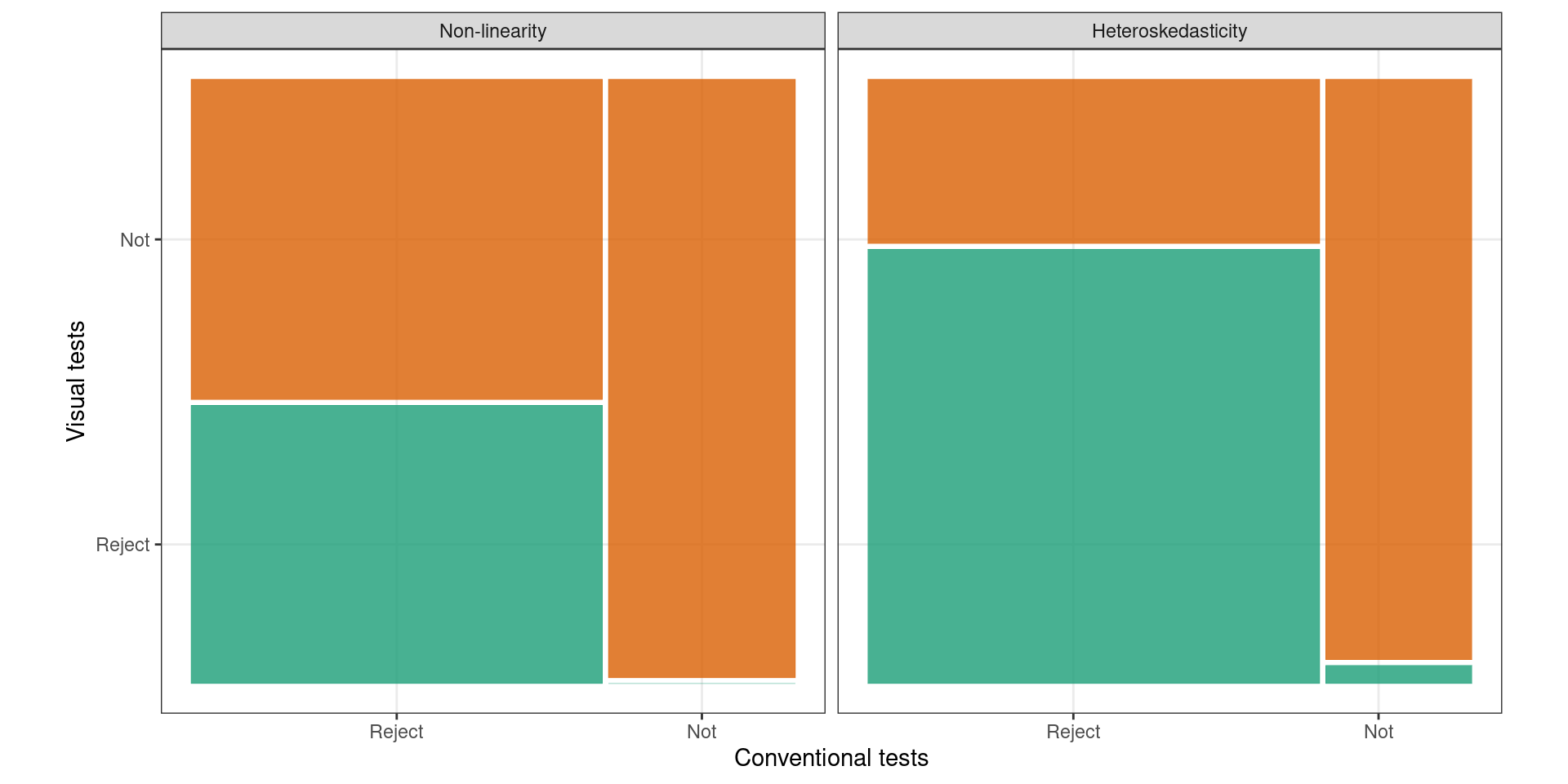
🪩 The Oddball Dataset

• Plot 17 is the target

📓 Conclusions

Visual Test

• One test, multiple violations

Conventional Test

• Multiple tests required

Violation	Test
nonlinearity	RESET
heteroskedasticity	Breusch-Pagan
goodness-of-fit	Shapiro-Wilk

📓 Conclusions

Visual Test

• One test, multiple violations
• Reject ➡️
  • severe issue w/ model fit

Conventional Test

• Multiple tests required
• Reject ➡️
  • minor issue, no model impact OR
  • major issue, model impact (no way to tell)

📓 Conclusions

Visual Test

• One test, multiple violations
• Reject ➡️
  • severe issue w/ model fit
  • 99.99% chance conventional test also rejects

Conventional Test

• Multiple tests required
• Reject ➡️
  • minor issue, no model impact OR
  • major issue, model impact (no way to tell)

⚠️ Limitations of Lineup Protocol

1. Humans cannot (easily) evaluate

• lineups w/ many plots

• a large number of lineups

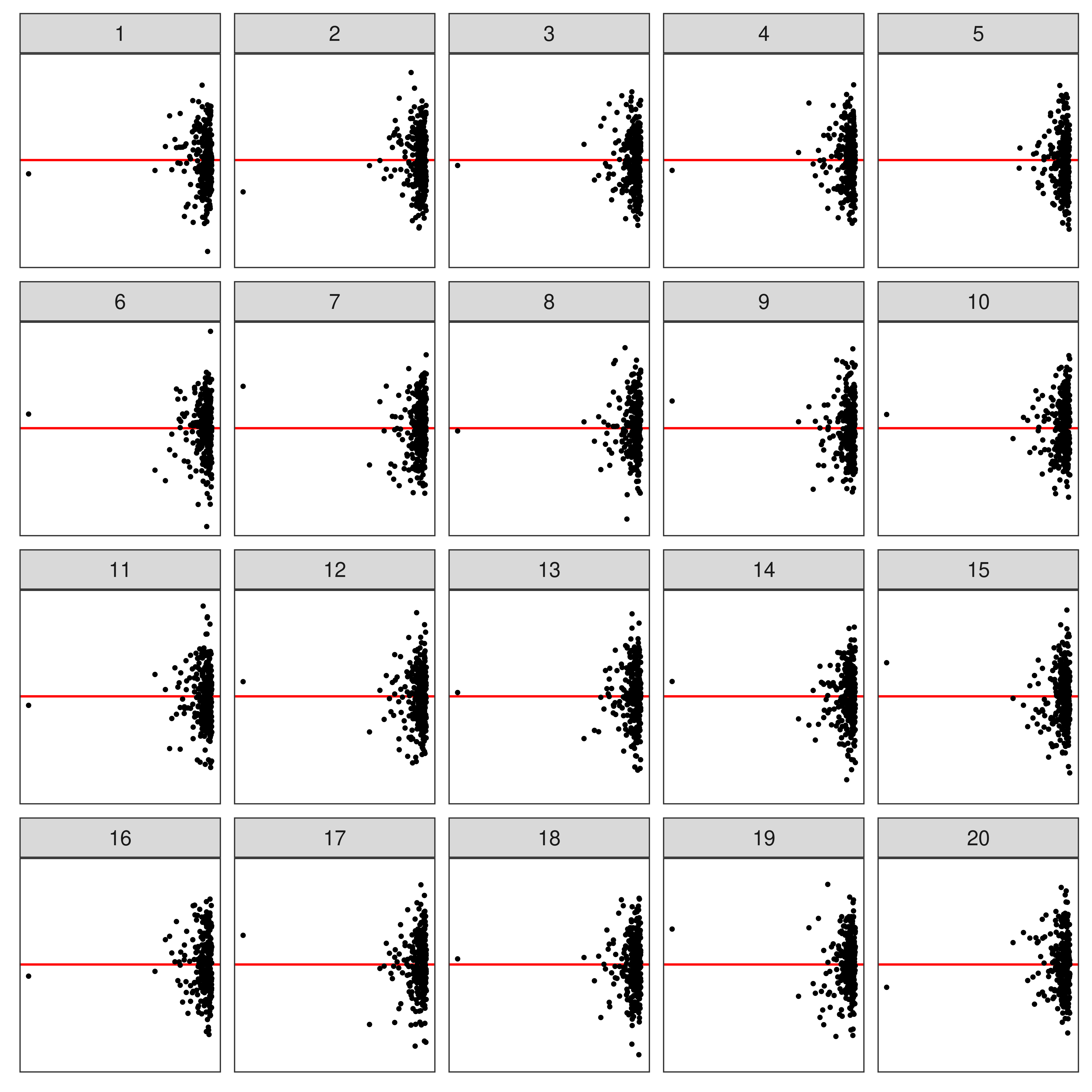
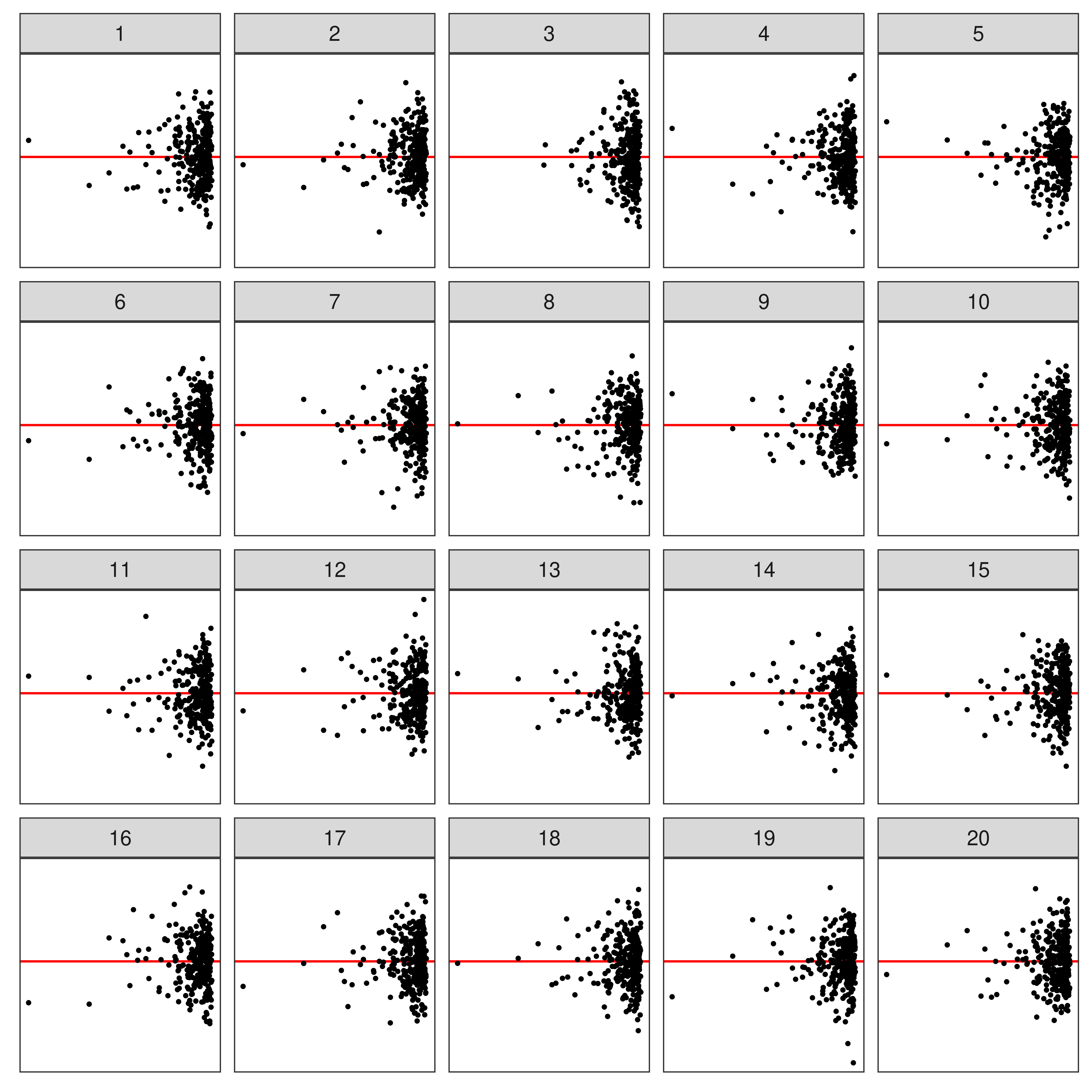
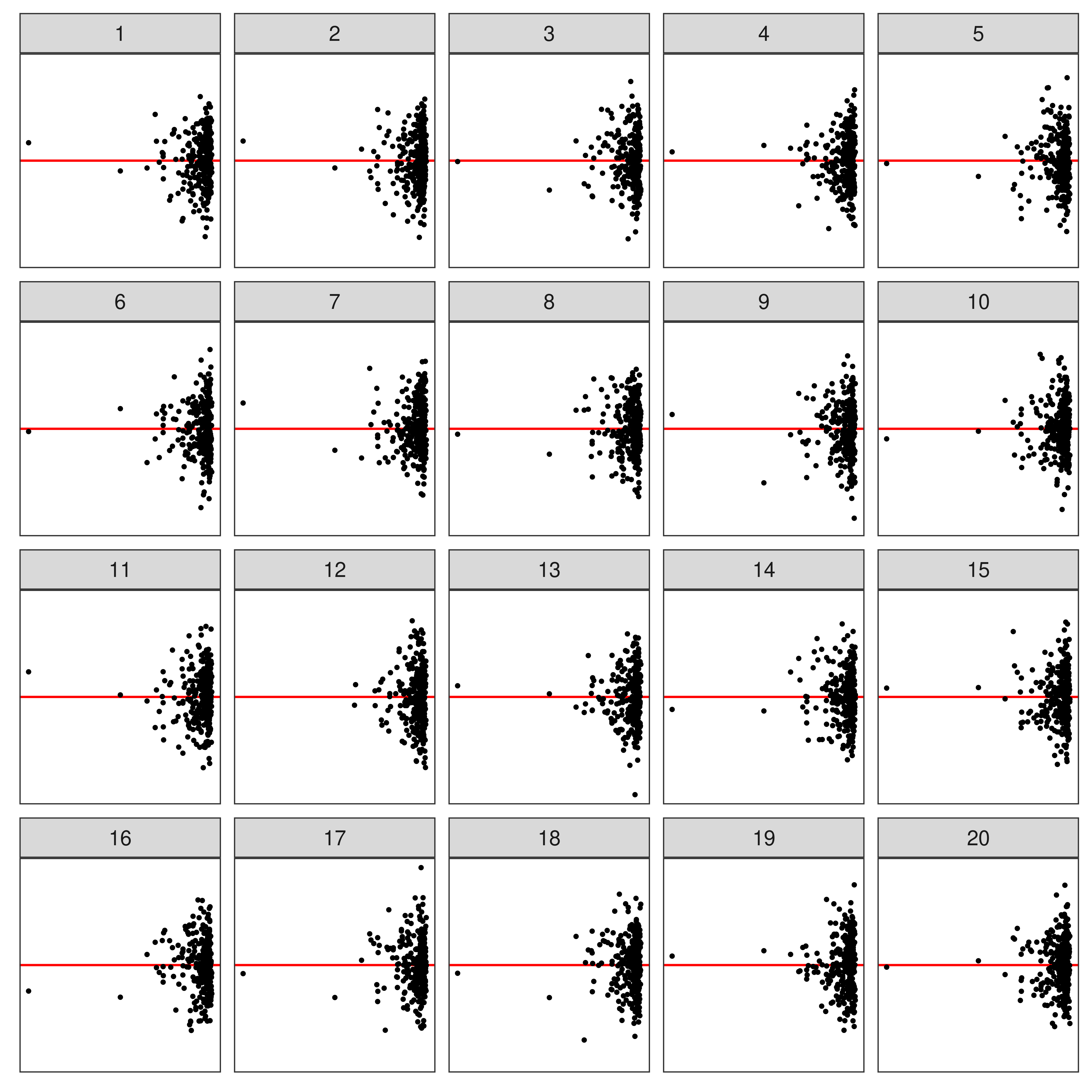
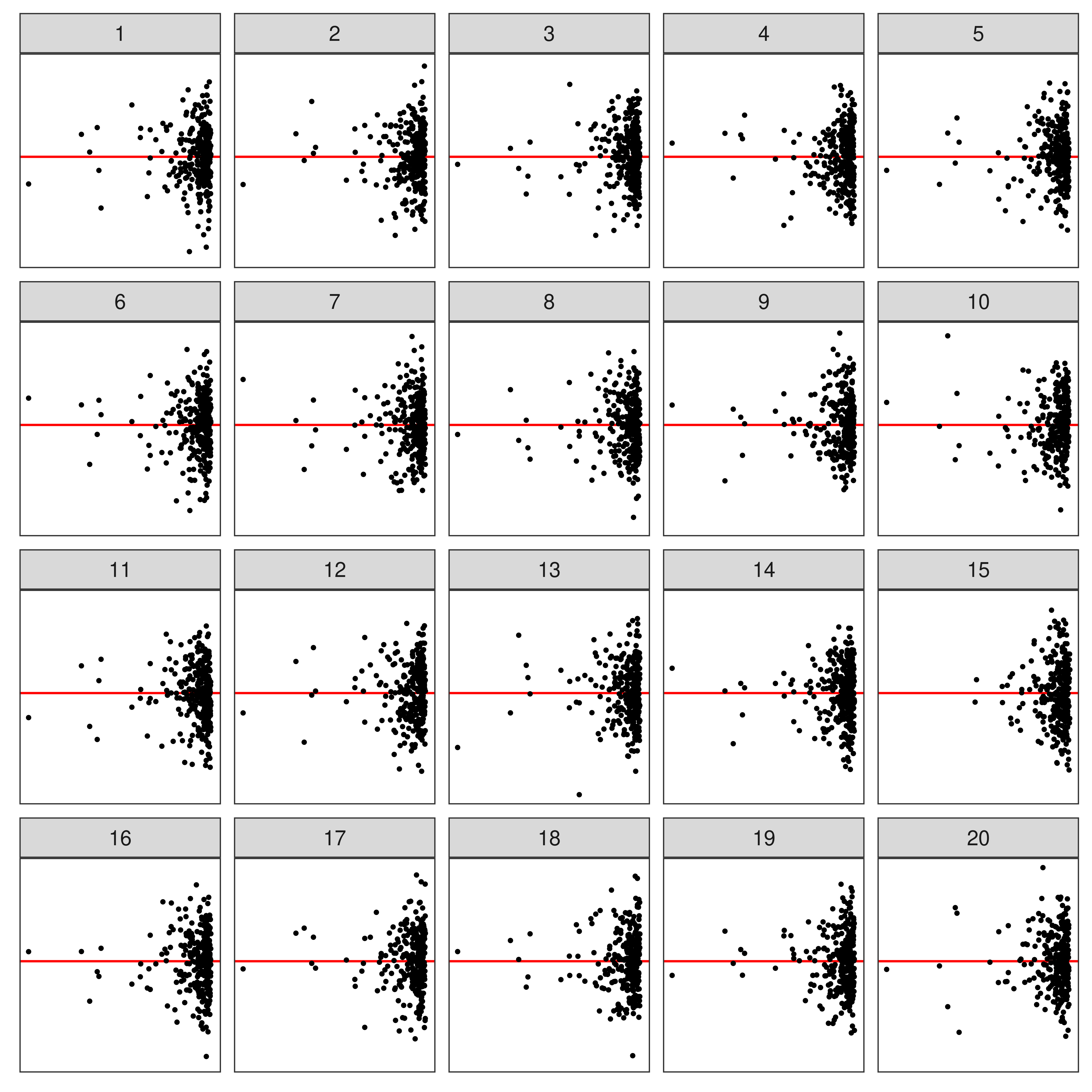
⚠️ Limitations of Lineup Protocol

1. Humans cannot (easily) evaluate
   • lineups w/ many plots
   • a large number of lineups

2. Lineups have 💰 high labor costs and can be 🕑 time consuming to evaluate

➡️ Make the 🖥️ do it for us with 🪄Computer Vision 🤖

🤖 AutoVI: Automated Assessment of Residual Plots with Computer Vision

🛣️ Roadmap

1. Estimate ‘visual’ distance \(D\) between

   • an actual residual plot
   • a plot of residuals generated under the null model

2. Compare \(\widehat D\) to a distribution of values

3. Calibrate against visual and conventional test results

📏 Measuring Distance

How to measure “difference”/“distance” between plots?

• Statistics: KL-Divergence (actual vs. null) when data generating process is known
• Graphics: scagnostics
• Image Analysis:
  • pixel-wise sum of square differences
  • Structural Similarity Index Measure (SSIM)

🎯 Estimating Distance

\(\widehat{D} = f_{CV}(V_{h \times w}(\boldsymbol{e}), n, S(\hat y, \hat e))\), where

• \(V_{h \times w}(.)\) is a \(h\times w\) image
• \(n\) observations
• \(S(\hat y, \hat e)\) are Scagnostics
• Computer Vision algorithm \(f_{CV}(.) \rightarrow [0, +\infty)\)

💡Training: Model Violations

Non-linearity + Heteroskedasticity

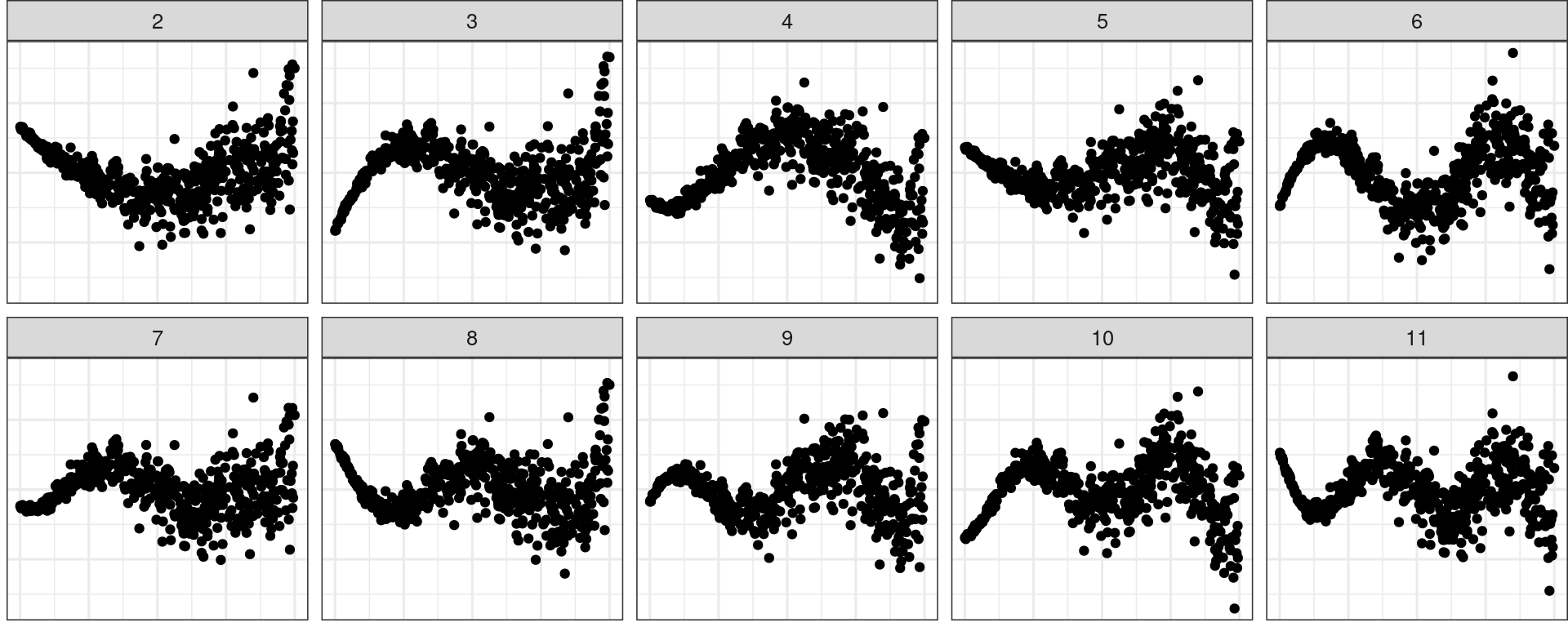
Non-normality + Heteroskedasticity

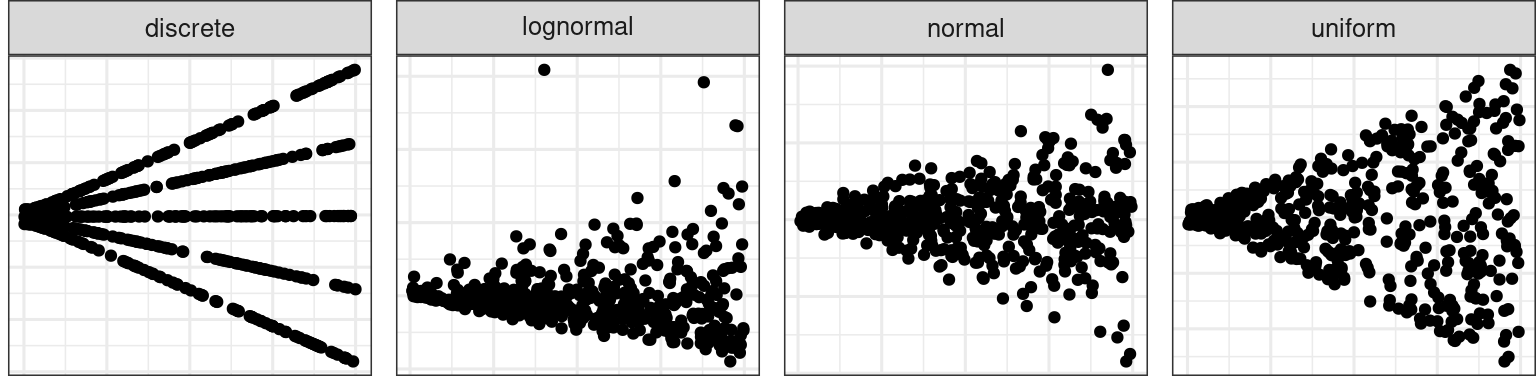
💡Training: Predictor Distribution

Distribution of predictor

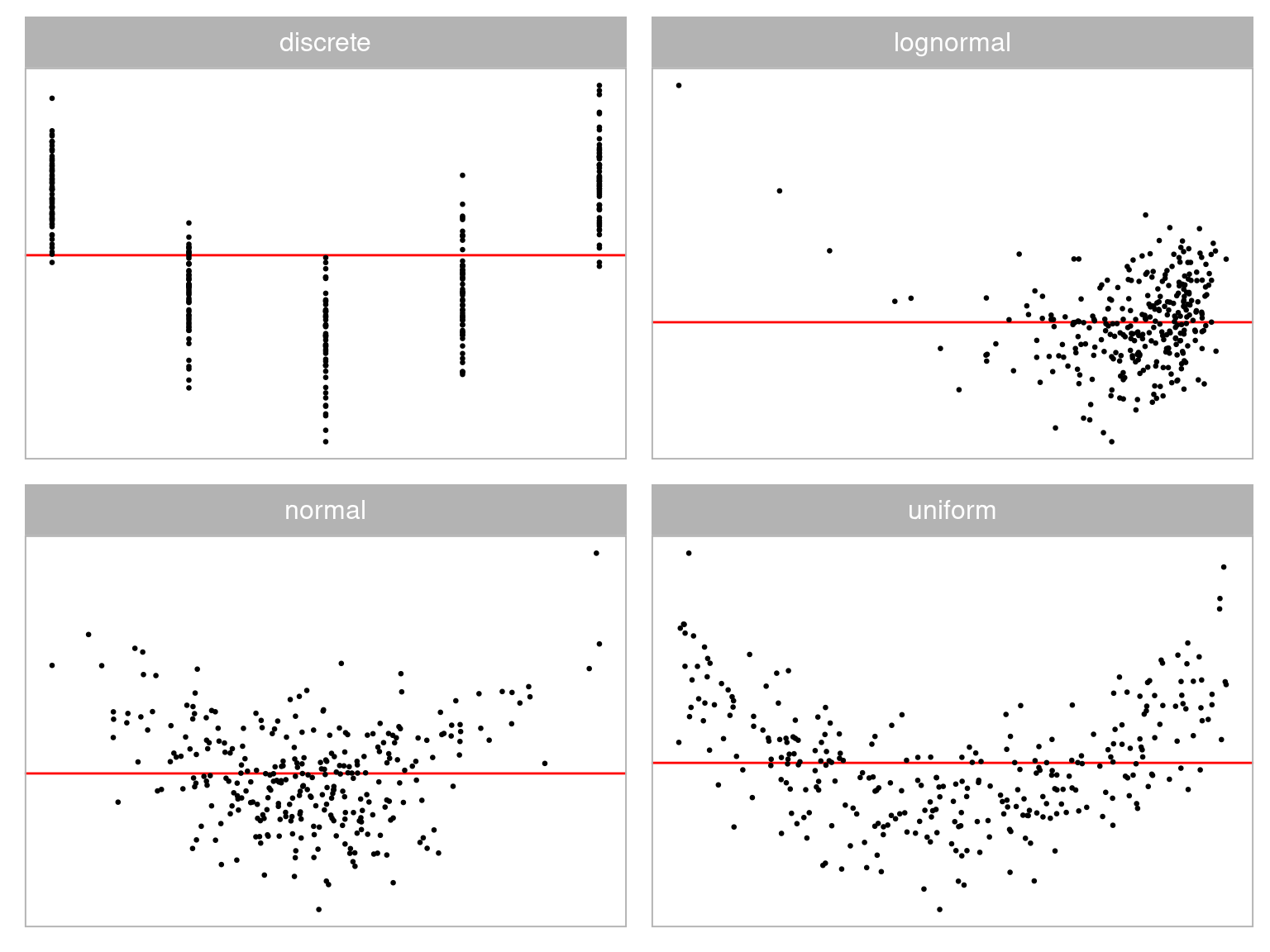
🔬Statistical Testing

• Estimate null distribution \(F(D | H_0)\) empirically:

  • Generate data under \(H_0\)
  • Calculate \(\widehat{D}\)

• Compute critical value \(Q_0(0.95)\) as the value \(Q\) s.t. \(F(D \leq Q | H_0) = 0.95\)

• \(p\)-value: \(P(D \geq D^\ast)\) for observed \(D^\ast\)

Comparison to Visual Inference

• Each lineup used in the experiment has 1 target and 19 null plots
• Run each plot through the model to get \(\widehat D\) (+ RESET & BP tests)
• Compare performance metrics

Comparison to Visual Inference

AutoVI is in between conventional and lineup tests in terms of conservatism. Lineups are still much more likely to not reject than AutoVI, but it is at least a step in the right direction.

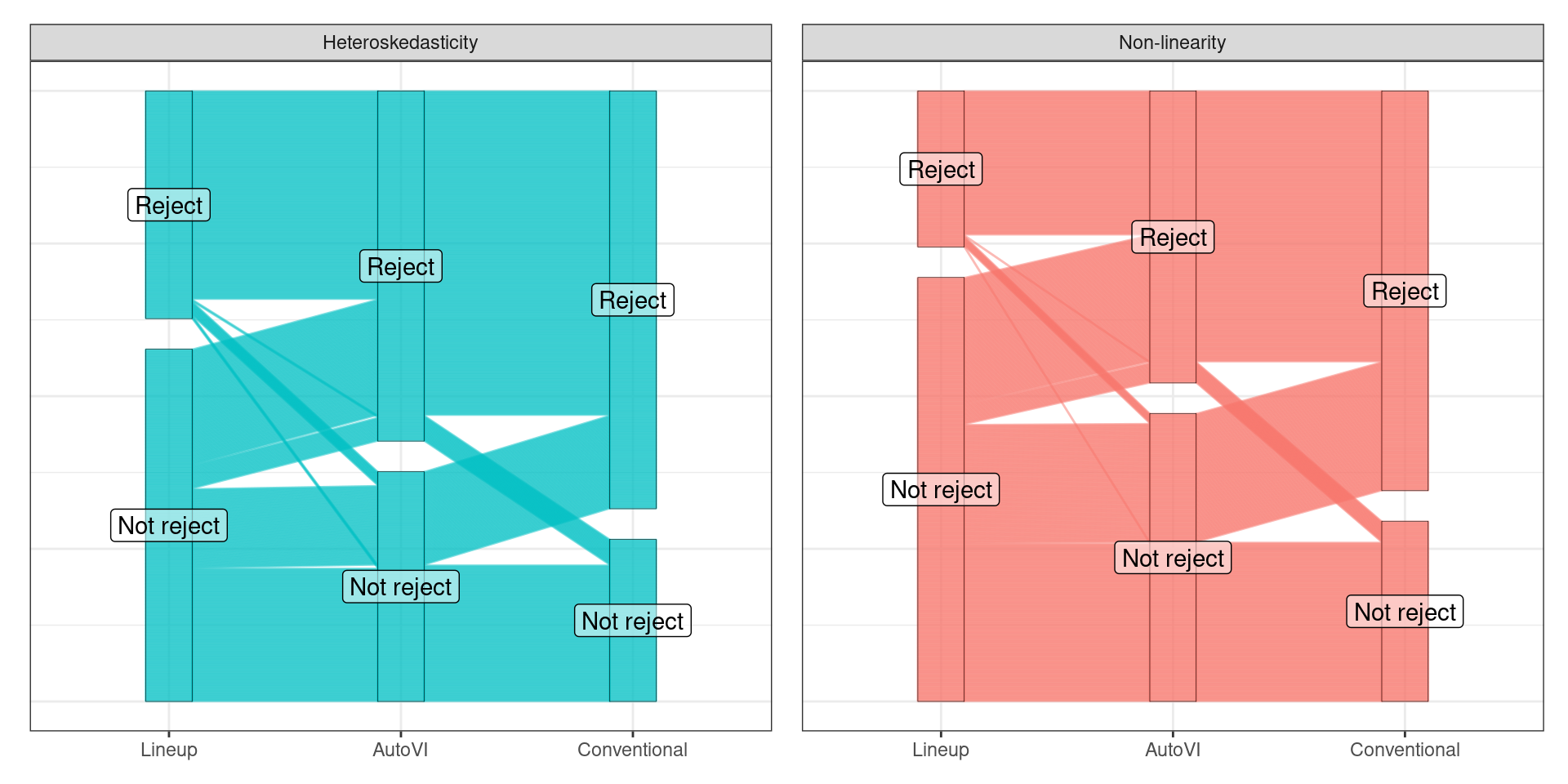
autovi Package

The autovi package provides automated visual inference with computer vision models. It is available on CRAN and Github.

Core Methods

• Null residuals simulation: rotate_resid()
• Visual signal strength: vss()
• Comprehensive checks: check() and summary_plot()

💡Example: Boston Housing

Normal view

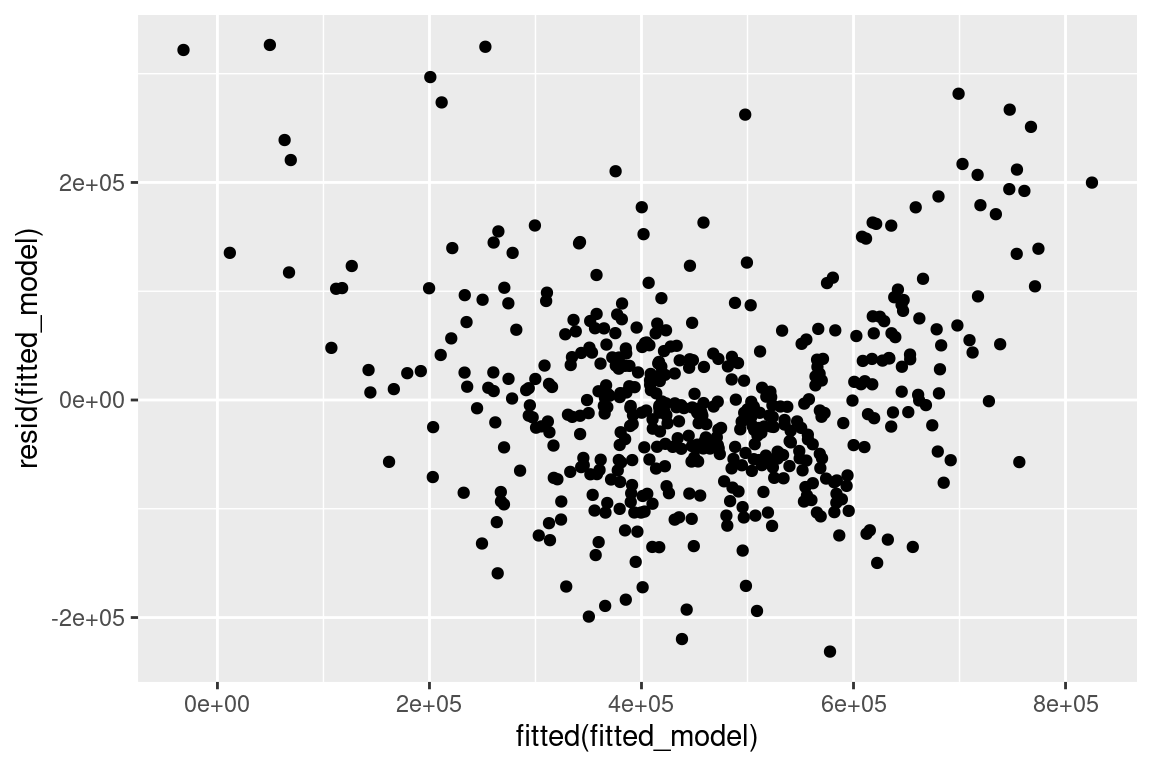
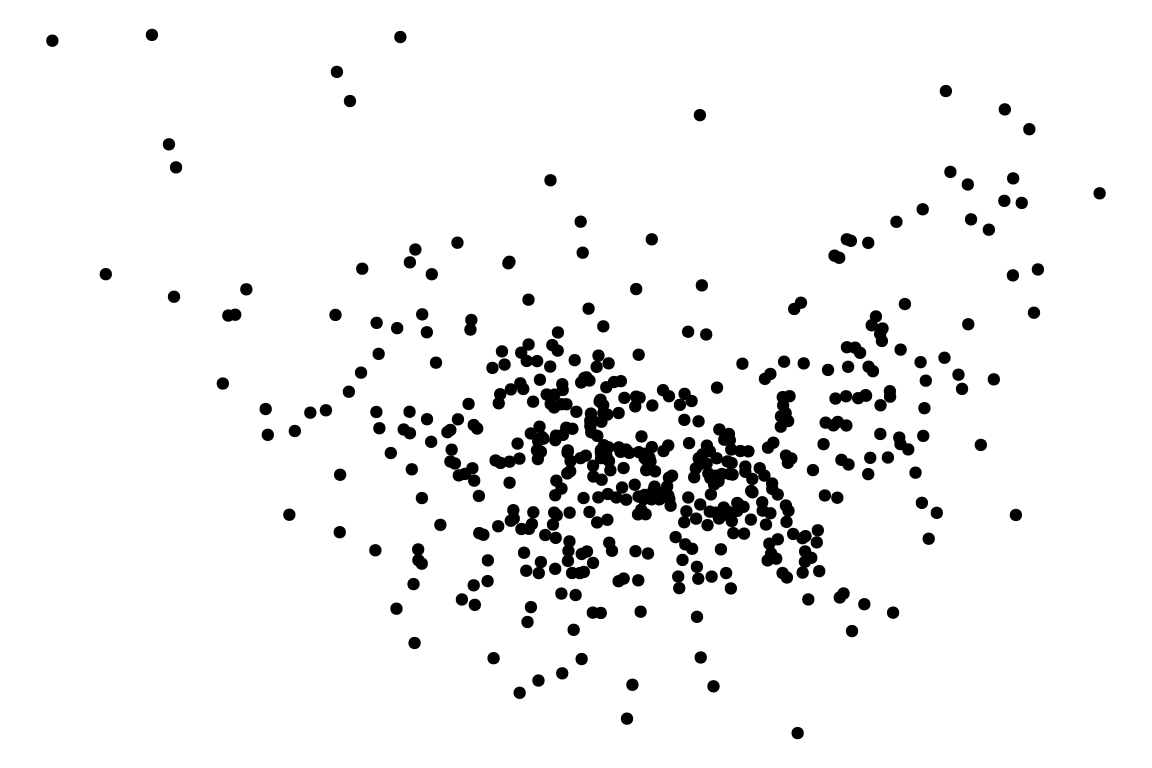
Pass into autovi

💡Example: Boston Housing

Null residuals are simulated from the fitted model assuming it is correctly specified.

checker <- auto_vi(fitted_model = fitted_model, 
                   keras_model = get_keras_model("vss_phn_32"))
checker$rotate_resid()

# A tibble: 489 × 2
   .fitted   .resid
     <dbl>    <dbl>
 1 632372.   24372.
 2 525177.   13236.
 3 646753.   54824.
 4 624848.  -98465.
 5 611817.  188264.
 6 551051.  -67975.
 7 504757.  142250.
 8 445700. -175323.
 9 281912. -101298.
10 453398. -121730.
# ℹ 479 more rows

checker$rotate_resid() |>
  checker$plot_resid()

:::

vss()

Visual signal strength of the actual residual plot

checker$vss()

✔ Predict visual signal strength for 1 image.

# A tibble: 1 × 1
    vss
  <dbl>
1  6.48

Visual signal strength comparison

checker$summary_plot()

check()

checker$check()
checker

── <AUTO_VI object>
Status:
 - Fitted model: lm
 - Keras model: (None, 32, 32, 3) + (None, 5) -> (None, 1)
    - Output node index: 1
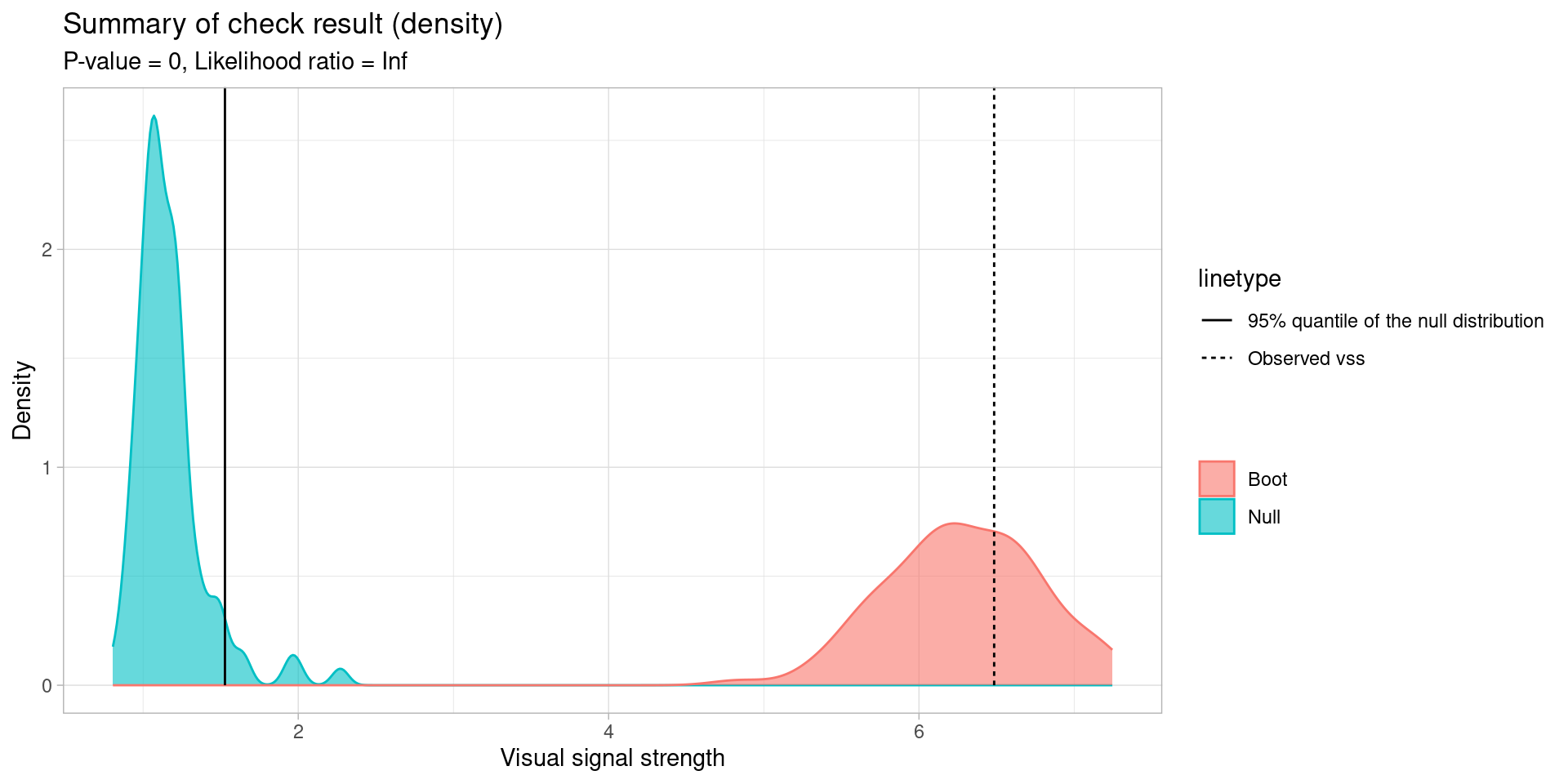
 - Result:
    - Observed visual signal strength: 6.484 (p-value = 0)
    - Null visual signal strength: [100 draws]
       - Mean: 1.169
       - Quantiles: 
          ╔══════════════════════════════════════════╗
          ║  25%   50%   75%   80%   90%   95%   99% ║
          ║1.037 1.120 1.231 1.247 1.421 1.528 1.993 ║
          ╚══════════════════════════════════════════╝
    - Bootstrapped visual signal strength: [100 draws]
       - Mean: 6.28 (p-value = 0)
       - Quantiles: 
          ╔══════════════════════════════════════════╗
          ║  25%   50%   75%   80%   90%   95%   99% ║
          ║5.960 6.267 6.614 6.693 6.891 7.112 7.217 ║
          ╚══════════════════════════════════════════╝
    - Likelihood ratio: 0.7064 (boot) / 0 (null) = Extremely large 

💡Example: Dinosaur

RESET \(p\)-value = 0.742
B-P \(p\)-value = 0.36
S-W \(p\)-value = 9.21e-05

:::

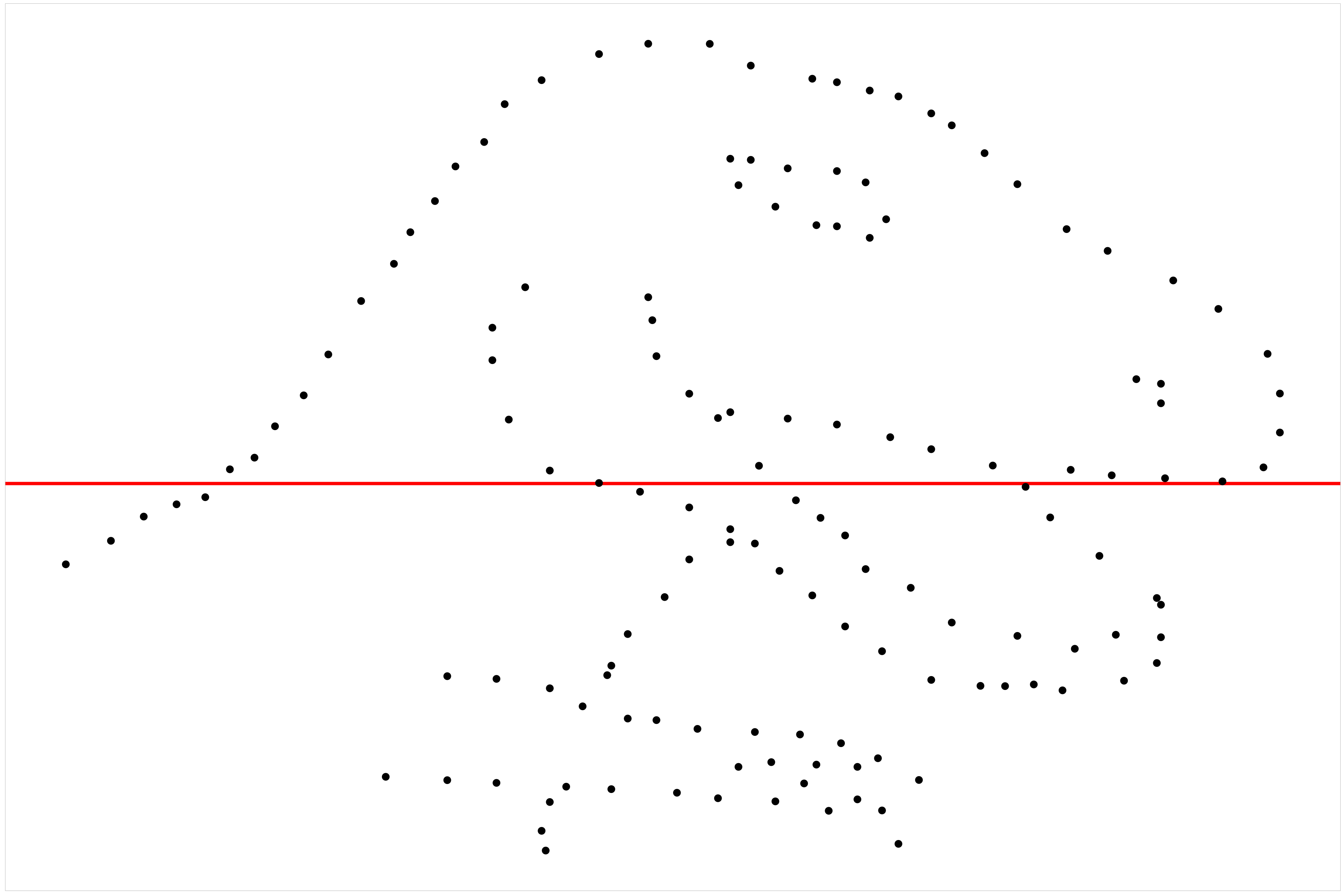
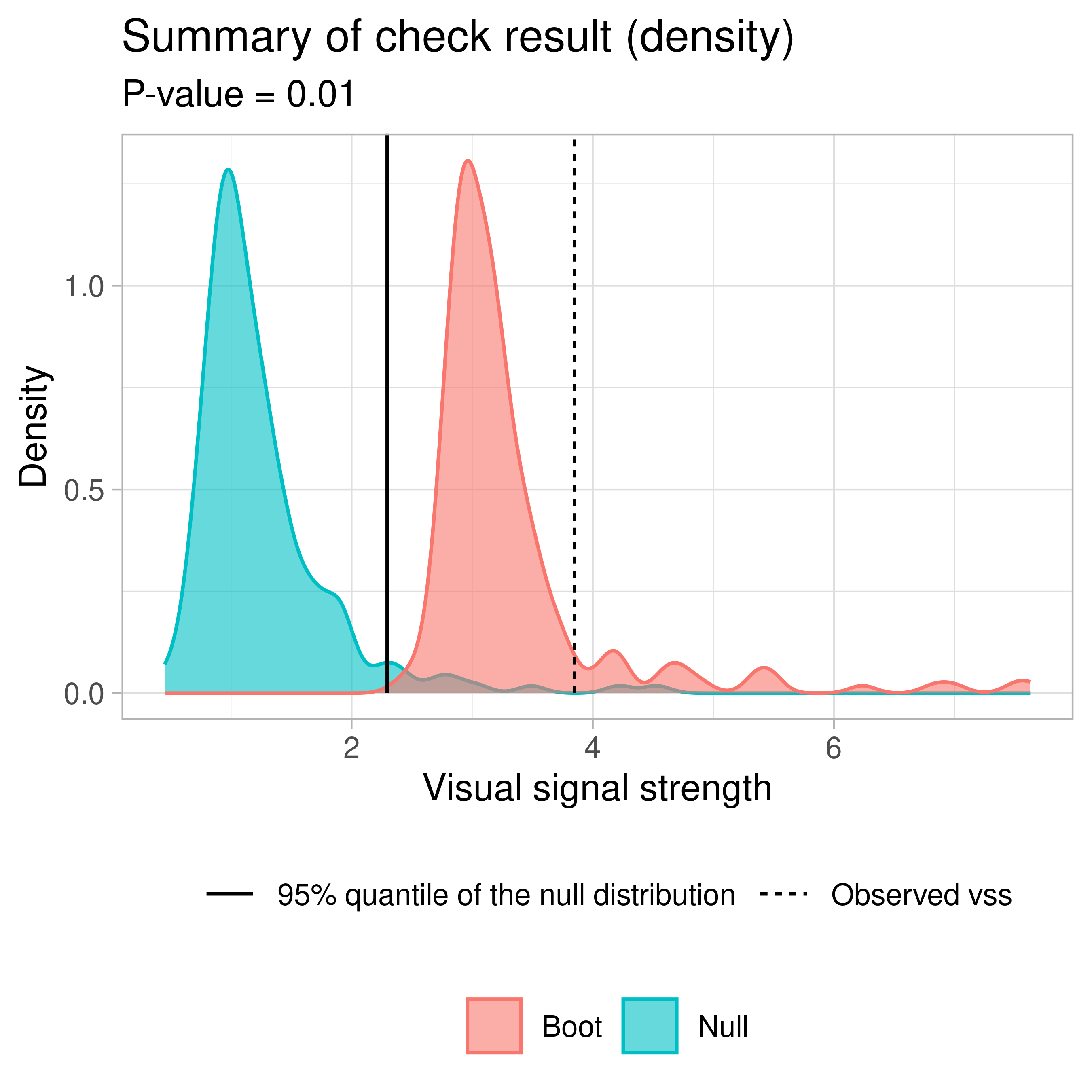
🌐Shiny Application

Don’t want to install TensorFlow?

Try our shiny web application: https://shorturl.at/DNWzt

🧩Extensions

For GLMs and other regression models:

1. Use raw residuals, but violations may not be identifiable and the test could be two-sided.
2. Use transformed residuals that are roughly normally distributed.
3. Reuse the pre-trained convolutional blocks and train a new computer vision model with an appropriate distance measure.

🎬Takeaway

You can use autovi to

• Evaluate lineups of residual plots of linear regression models

• Capture the magnitude of model violations through visual signal strength

• Automatically detect model misspecification using a visual test

Thanks! Any questions?

Weihao (Patrick) Li

did all of the 🦾 work

tengmcing

patrick.li@monash.edu

📦 autovi

Advisors

Di Cook

Emi Tanaka

Klaus Ackermann

References

Belsley, David A., Edwin Kuh, and Roy E. Welsch. 1980. Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. 14. [pr.]. Wiley Series in Probability and Mathematical Statistics. New York: Wiley.

Buja, Andreas, Dianne Cook, Heike Hofmann, Michael Lawrence, Eun-Kyung Lee, Deborah F Swayne, and Hadley Wickham. 2009. “Statistical Inference for Exploratory Data Analysis and Model Diagnostics.” Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 367 (1906): 4361–83. https://doi.org/10.1098/rsta.2009.0120.

Cook, R. Dennis, and Sanford Weisberg. 1982. “Criticism and Influence Analysis in Regression.” Sociological Methodology 13: 313–61. https://doi.org/10.2307/270724.

Draper, N. R., and H. Smith. 1998. Applied Regression Analysis. 1st ed. Wiley Series in Probability and Statistics. Hoboken, NJ: Wiley. https://books.google.com/books?id=d6NsDwAAQBAJ.

Mason, Harriet, Stuart Lee, Ursula Laa, and Dianne Cook. 2024. “Numbats/Cassowaryr.” NUMBATS: Non-Uniform Monash Business Analytics Team repo for joint projects. https://github.com/numbats/cassowaryr.

Montgomery, Douglas C., and Elizabeth A. Peck. 1982. Introduction to Linear Regression Analysis. Hoboken, NJ: John Wiley & Sons.

VanderPlas, Susan, Christian Röttger, Dianne Cook, and Heike Hofmann. 2021. “Statistical Significance Calculations for Scenarios in Visual Inference.” Stat 10 (1). https://doi.org/10.1002/sta4.337.