9 Mathematical and Logical Operators

Published

April 21, 2025

9.1 Objectives

Understand and use mathematical operators for mathematical computation
Understand and use logical operators to evaluate complex conditions
Understand and use basic string operations (repetition and concatenation)
Evaluate expressions using order of operations to predict how the computer will execute code
Translate mathematical concepts into a series of computational operations

9.2 Mathematical Operators

Let’s first start with a special class of functions that you’re probably familiar with from your math classes - mathematical operators.

Here are a few of the most important ones:

Table 9.1: Mathematical operators in R and Python

Operation	R symbol	Python symbol
Addition	`+`	`+`
Subtraction	`-`	`-`
Multiplication	`*`	`*`
Division	`/`	`/`
Integer Division	`%/%`	`//`
Modular Division	`%%`	`%`
Exponentiation	`^`	`**`

These operands are all for scalar operations (operations on a single number) - vectorized versions, such as matrix multiplication, are somewhat more complicated (and different between R and python).

Example: Integer and Modular Division

Integer division is the whole number answer to A/B, and modular division is the fractional remainder when A/B.

Let’s demonstrate with the problem 14/3, which evaluates to 4.6666667 when division is used, but has integer part 4 and remainder 2.

R
Python

14 %/% 3 in R would be 4, and 14 %% 3 in R would be 2.

14 %/% 3
## [1] 4
14 %% 3
## [1] 2

14 // 3
## 4
14 % 3
## 2

9.3 Order of Operations

Both R and Python operate under the same mathematical rules of precedence that you learned in school. You may have learned the acronym PEMDAS, which stands for Parentheses, Exponents, Multiplication/Division, and Addition/Subtraction. That is, when examining a set of mathematical operations, we evaluate parentheses first, then exponents, and then we do multiplication/division, and finally, we add and subtract.

R
Python

(1+1)^(5-2)
1 + 2^3 * 4
3*1^3
## [1] 8
## [1] 33
## [1] 3

1: The items in parentheses are evaluated first, so the expression becomes (2)^(3). Then, exponentiation is performed, yielding 8.
2: Exponentiation is performed first (PEMDAS), so the expression becomes 1 + 8*4. Then multiplication is performed, yielding 1 + 32. Addition is the final step, so we get 33.
3: Exponentiation is performed first, so this becomes 3*1. Then multiplication is performed, producing a final result of 3.

(1+1)**(5-2)
1 + 2**3*4
3*1**3
## 8
## 33
## 3

1: The items in parentheses are evaluated first, so the expression becomes (2)^(3). Then, exponentiation is performed, yielding 8.
2: Exponentiation is performed first (PEMDAS), so the expression becomes 1 + 8*4. Then multiplication is performed, yielding 1 + 32. Addition is the final step, so we get 33.
3: Exponentiation is performed first, so this becomes 3*1. Then multiplication is performed, producing a final result of 3.

9.4 Simple String Operations

Python has some additional operators that work on strings. In R, you will have to use functions to perform these operations, as R does not have string operators.

In Python, + will concatenate (stick together) two strings. Multiplying a string by an integer will repeat the string the specified number of times.

"first " + "second"
## 'first second'
"hello " * 3
## 'hello hello hello '

In R, to concatenate things, we need to use functions: paste or paste0:

paste("first", "second", sep = " ")
paste("first", "second", collapse = " ")
paste(c("first", "second"), sep = " ") # sep only works w/ 2 objects passed in
paste(c("first", "second"), collapse = " ") # collapse works on vectors

paste(c("a", "b", "c", "d"), 
      c("first", "second", "third", "fourth"), 
      sep = "-", collapse = " ")
# sep is used to collapse parameters, then collapse is used to collapse vectors

paste0(c("a", "b", "c"))
paste0("a", "b", "c") # equivalent to paste(..., sep = "")
## [1] "first second"
## [1] "first second"
## [1] "first"  "second"
## [1] "first second"
## [1] "a-first b-second c-third d-fourth"
## [1] "a" "b" "c"
## [1] "abc"

You don’t need to understand the details of this code at this point in the class, but it is useful to know how to combine strings in both languages.

9.5 Logical Operators

Logical variables can be combined through the use of logical operators in much the same way that numerical variables are combined through mathematical operators.

There are specific logical operators which are used to aggregate and combine multiple logical variables: the primary logical operators are and, or, and not ¹.

In pseudocode, which is human-readable logic structured like computer code but without the syntax, we usually write these out in all caps.

(X AND Y) requires that both X and Y are true.
(X OR Y) requires that one of X or Y is true.
(NOT X) is true if X is false, and false if X is true. Sometimes called negation.
(X XOR Y) requires that one (and only one) of X or Y is true. Sometimes called exclusive or.

Truth Tables: Useful Tools for Understanding Logical Expressions

When constructing a logical expression that combines Boolean variables, it can be helpful to build a truth table that lists all possible inputs on the left and the output of the operator on the right. A truth table demonstrating the logical operators and, or, not and xor is provided in Table 9.2.

Table 9.2: Truth table for each of the common logical operators.

a	b	a `and` b	a `or` b	`not` a	`not` b	a `xor` b
T	T	T	T	F	F	F
T	F	F	T	F	T	T
F	T	F	T	T	F	T
F	F	F	F	T	T	F

Table 9.3: Logical operators in R and Python. These operators are intended for single values; evaluation of vectors may require different operators. Note the use of ^ for xor in Python!

Operation	R	Python
and	`&`	`&` or `and`
or	`\|`	`\|` or `or`
not	`!`	`not`
xor	`xor()`	`^`

When writing code, we use the logical operators in R and Python shown in Table 9.3.

Exploring Logical Operators with R and Python

We can generate each entry in the truth table using the relevant logical operators in R and python.

In R, and comparisons use & as the operator.


TRUE & TRUE
## [1] TRUE
TRUE & FALSE
## [1] FALSE
FALSE & TRUE
## [1] FALSE
FALSE & FALSE
## [1] FALSE

In Python, and expressions use & as the operator.

True & True
## True
True & False
## False
False & True
## False
False & False
## False

Alternately, in Python, you can also spell out the whole word and use and explicitly.

True and True
## True
True and False
## False
False and True
## False
False and False
## False

In R, or is denoted with | (the vertical bar, shift + the button above the enter key on most keyboards).

TRUE | TRUE
## [1] TRUE
TRUE | FALSE
## [1] TRUE
FALSE | TRUE
## [1] TRUE
FALSE | FALSE
## [1] FALSE

In Python, or expressions use | as the operator.

True | True
## True
True | False
## True
False | True
## True
False | False
## False

Alternately, in Python, you can also spell out the whole word and use or explicitly.

True or True
## True
True or False
## True
False or True
## True
False or False
## False

In R, negation occurs using the ! operator.

!TRUE
## [1] FALSE
!FALSE
## [1] TRUE

In Python, negation occurs using the not operator.

not True
## False
not False
## True

In R, exclusive or uses the xor() function.

xor(TRUE, TRUE)
## [1] FALSE
xor(TRUE, FALSE)
## [1] TRUE
xor(FALSE, TRUE)
## [1] TRUE
xor(FALSE, FALSE)
## [1] FALSE

In Python, exclusive or uses the ^ operator.

True ^ True
## False
True ^ False
## True
False ^ True
## True
False ^ False
## False

Note that this is why the exponentiation operator in Python is ** instead of ^. Using ^ may produce errors (TypeError: unsupported operand type(s)) or may produce unexpected results with no warning at all, as in the following example.

3^4
## 7

9.5.1 Order of Operations

Just as with mathematical operators, there is an order of operations to logical operators.

Precedence order: (top is evaluated first)

R
Python

a1 <- TRUE
b1 <- FALSE
c1 <- FALSE

a1 | b1 & c1 # AND takes precedence
## [1] TRUE
a1 | (b1 & c1) # same as above, with parentheses
## [1] TRUE
(a1 | b1) & c1 # force OR to be first using parentheses
## [1] FALSE

a1 = True
b1 = False
c1 = False

a1 or b1 and c1 # AND takes precedence
## True
a1 or (b1 and c1) # same as above, with parentheses
## True
(a1 or b1) and c1 # force OR to be first using parentheses
## False

9.5.2 De Morgan’s Laws

De Morgan’s Laws are a set of rules for how to combine logical statements, similar to distributive laws in numerical operations. You can represent them in a number of ways:

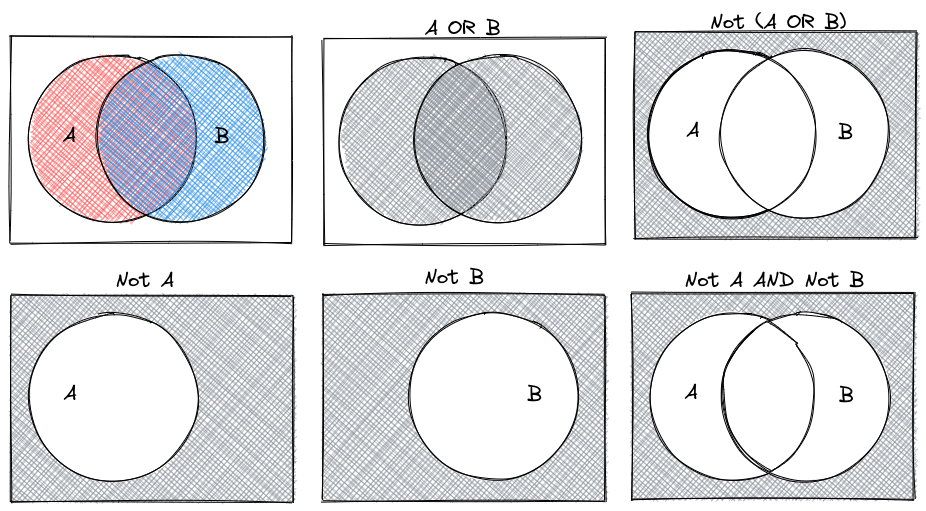
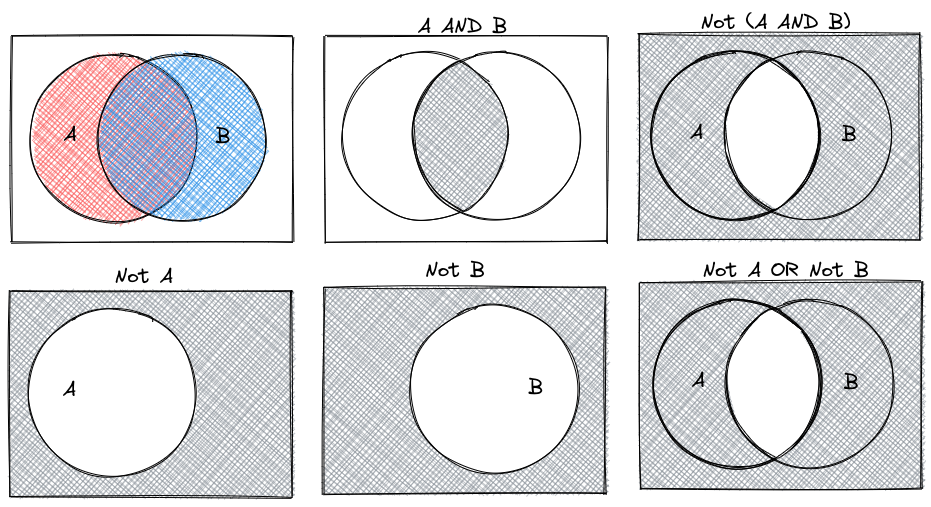
NOT(A or B) is equivalent to NOT(A) and NOT(B)
NOT(A and B) is equivalent to NOT(A) or NOT(B)

Visual Representation of DeMorgan’s Laws

We can also represent De Morgan’s Laws visually using Venn Diagrams.

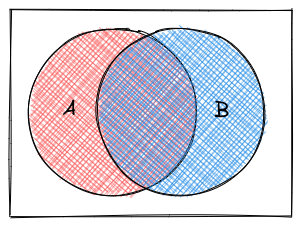
We will use the convention that .

DeMorgan’s First Law

A venn diagram illustration of De Morgan’s laws showing that the region that is outside of the union of A OR B (aka NOT (A OR B)) is the same as the region that is outside of (NOT A) and (NOT B)

R
Python

!(TRUE | TRUE)
## [1] FALSE
!(TRUE | FALSE)
## [1] FALSE
!(FALSE | TRUE)
## [1] FALSE
!(FALSE | FALSE)
## [1] TRUE

!TRUE & !TRUE
## [1] FALSE
!TRUE & !FALSE
## [1] FALSE
!FALSE & !TRUE
## [1] FALSE
!FALSE & !FALSE
## [1] TRUE

not(True or True)
## False
not(True or False)
## False
not(False or True)
## False
not(False or False)
## True

not(True) and not(True)
## False
not(True) and not(False)
## False
not(False) and not(True)
## False
not(False) and not(False)
## True

DeMorgan’s Second Law

A venn diagram illustration of De Morgan’s laws showing that the region that is outside of the union of A AND B (aka NOT (A AND B)) is the same as the region that is outside of (NOT A) OR (NOT B)

R
Python

!(TRUE & TRUE)
## [1] FALSE
!(TRUE & FALSE)
## [1] TRUE
!(FALSE & TRUE)
## [1] TRUE
!(FALSE & FALSE)
## [1] TRUE

!TRUE | !TRUE
## [1] FALSE
!TRUE | !FALSE
## [1] TRUE
!FALSE | !TRUE
## [1] TRUE
!FALSE | !FALSE
## [1] TRUE

not(True and True)
## False
not(True and False)
## True
not(False and True)
## True
not(False and False)
## True

not(True) or not(True)
## False
not(True) or not(False)
## True
not(False) or not(True)
## True
not(False) or not(False)
## True

A fourth commonly used logical operator is exclusive or (xor). xor is True if only one of the two conditions is True, but False if both are True. xor is not a basic boolean operator, as it can be written as a combination of other operators: A xor B = (A or B) and not(A and B).↩︎